こんにちは、こんぶちゃです!
私はCourseraで提供されているStanford University & DeepLearning.AIによるMachine Learning コースを受講しました。そのコースで学んだ内容を基に、ストーリー仕立てで、より楽しく、かつ理解しやすい形で機械学習の基礎を解説していきます。
- AIがどのように「考え」、動作するのかの裏側に興味がある方
- 機械学習の基本的な概念やアルゴリズムをゼロから学びたい方
- Pythonを使って、機械学習のモデルを自分で手を動かして実装してみたい方
この記事を通じて、機械学習の魅力的な世界への第一歩を踏み出しましょう。早速、始めていきましょう。
はじめに:ライナー君の新たな挑戦
皆さん、こんにちは!前回の冒険で、ライナー君は線形回帰を使ってデータの謎を解き明かしました。でも、現実世界はもっと複雑ですよね?そこで、ライナー君は新たな挑戦に立ち向かいます:重回帰分析です!
「重回帰分析ってなに?」と思うかもしれませんね。簡単に言うと、これは複数の独立変数(入力)を使用して、依存変数(出力)を予測する方法です。つまり、ライナー君は今回、一つではなく、複数の道具(変数)を駆使して、宝(予測結果)を探し出します。
なぜ線形回帰からステップアップする必要があるのでしょう?それは、複数の要因が絡み合って結果に影響を与える現実世界をより正確に模倣するためです。例えば、家の価格を予測するには、面積だけでなく、部屋数や立地条件など、多くの要素を考慮する必要がありますよね。
ライナー君の使命は、このように複雑な現実世界のデータを扱い、より精度の高い予測を行うことです。彼は勇敢にもこの新しい冒険に挑む準備ができています。さあ、複数の変数を使って現実世界の予測に挑む、ライナー君の旅を一緒に追いかけましょう!
多次元の謎:重回帰分析とは?
ライナー君の新たな冒険が始まります。今回の挑戦は、一つではなく、複数の道具(独立変数)を使って、隠された宝(依存変数の予測値)を見つけ出すこと。それが重回帰分析の世界です。
重回帰分析の仕組み
重回帰分析では、複数の独立変数𝐗(例えば、家の面積、部屋数、立地など)を使って、一つの依存変数𝐲(例えば、家の価格)を予測します。
数学的には、重回帰分析は以下の式で表されます:
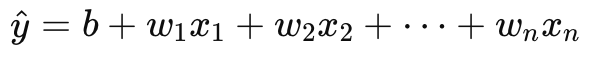
ここで、
- y^ (yハット) は予測される依存変数の値、
- 𝑏はバイアス(切片)、
- 𝐰1, 𝐰2, …, 𝐰𝑛は各独立変数の重み(パラメータ)、
- 𝑥1, 𝑥2, …, 𝑥𝑛は独立変数の値です。
この式は、ライナー君が持つ地図における宝への経路を示しています。各独立変数は宝を見つけるための異なる手がかりであり、その重みは手がかりの重要性を示しています。
最適化の旅:コスト関数と勾配降下法
ライナー君の冒険において、最も重要な試練の一つが「最適化の旅」です。この旅の目的は、重回帰分析モデルがデータに最もよくフィットするようにすることです。この目的を達成するための秘密の武器が、コスト関数と勾配降下法です。
コスト関数の役割
コスト関数(または損失関数)は、モデルの予測が実際のデータポイントからどれだけ離れているかを測定します。重回帰分析では、平均二乗誤差(MSE)が一般的に使用されるコスト関数です。式で表すと、以下のようになります:
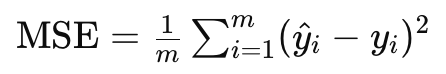
ここで、
- m はサンプル数です。
- y^i は予測値です。
- yi は実際の値です。
コスト関数の値が小さいほど、モデルの予測が実際のデータに近いことを意味します。
勾配降下法の魔法
勾配降下法は、コスト関数を最小化するための最適なパラメータ(wとb)を見つけるための方法です。この方法は、コスト関数の勾配(傾き)を計算し、その勾配が最小となる点に向かってパラメータを少しずつ更新していきます。
Pythonでの冒険の武器
ライナー君のPython装備には、コスト関数と勾配降下法を実装する力があります。以下は、勾配降下法を使用して重回帰分析モデルのパラメータを学習する簡単な例です:
コスト関数J:
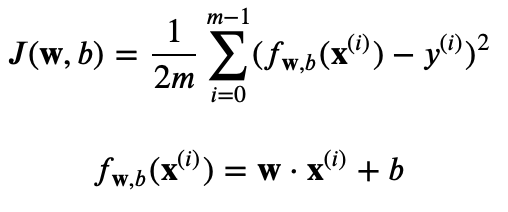
勾配降下方:
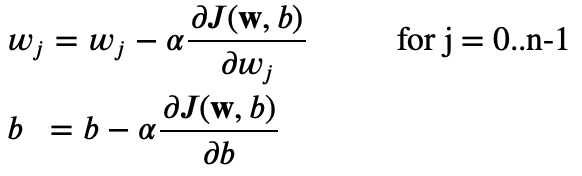
コスト関数Jの偏微分:
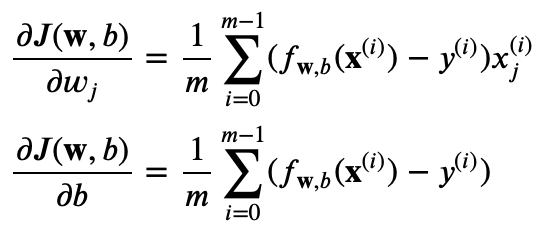
import numpy as np
def compute_cost(X, y, w, b):
m = len(y)
cost = 0
for i in range(m):
f_wb = np.dot(X[i], w) + b
cost += (f_wb - y[i]) ** 2
return cost / (2 * m)
def gradient_descent(X, y, w, b, alpha, num_iters):
m = len(y)
for i in range(num_iters):
dj_dw = np.zeros(len(w))
dj_db = 0
for j in range(m):
err = (np.dot(X[j], w) + b) - y[j]
for k in range(len(w)):
dj_dw[k] += err * X[j][k]
dj_db += err
w = w - alpha * (dj_dw / m)
b = b - alpha * (dj_db / m)
if i % 100 == 0: # 100イテレーションごとにコストを表示
print(f"Iteration {i}: Cost {compute_cost(X, y, w, b)}")
return w, bこのコードは、勾配降下法を使用して重回帰分析モデルのパラメータを最適化する過程を示しています。コスト関数の値を定期的に監視することで、モデルがどの程度改善しているかを追跡できます。
ライナー君のこの「秘密の武器」を使うことで、どんなに複雑なデータセットにも対応できる、強力な予測モデルを作り上げることができます。最適化の旅を通じて、ライナー君はデータの真実に近づいていきます。
scikit-learnの魔法:ライナー君の新たな武器
ライナー君の冒険における「最適化の旅」では、コスト関数と勾配降下法という重要な武器を手に入れました。これらは、ライナー君がデータの謎を解き明かし、予測の精度を高めるための強力な道具です。しかし、この旅はまだ終わりではありません。ライナー君はさらに強力で、使いやすい新たな魔法を手に入れることになります。それがscikit-learnです。
なぜscikit-learnなのか?
ライナー君がこれまでに学んだコスト関数の最小化や勾配降下法は、重回帰分析の背後にある数学を理解する上で非常に有益でした。しかし、多次元の冒険の世界では、より迅速かつ効率的に目的地へ到達する方法が求められます。ここでscikit-learnの魔法が登場します。
scikit-learnは、数多くの機械学習の呪文(アルゴリズム)を含む強力な魔法の書です。この魔法の書を使えば、ライナー君は複雑な計算を自ら行うことなく、データに最もフィットするモデルを見つけ出し、予測の精度を高めることができます。scikit-learnは、効率的に冒険を進め、より多くのデータの謎に挑むことを可能にします。
ライナー君の新たな挑戦
scikit-learnを手に入れたライナー君は、これまでの手動での魔法の呪文の唱え方(コーディング)から、もっと強力でスマートな魔法の使い方へと進化します。この新たな武器を使うことで、ライナー君は以前よりもずっと迅速に、そして効率的にデータの宝庫を探索できるようになります。
次のセクションでは、scikit-learnの魔法を使って、ライナー君がどのようにして新たなデータの地平へと旅を進めるのかを見ていきましょう。この新たな武器を駆使し、ライナー君と共にデータ分析の冒険をさらに深く探求していきます。
Pythonでライナー君を装備する
新たにscikit-learnの魔法の書を手に入れたライナー君は、これまでにない力を実感しています。重回帰分析の冒険では、適切な装備が不可欠ですが、pandasとscikit-learnライブラリがあれば、どんなデータの謎も解き明かすことができます。このセクションでは、ライナー君がどのようにしてこの新たな武器を使いこなし、データの前処理からモデルの訓練まで、重回帰分析の旅を進めるのかを見ていきましょう。
データの前処理
まず、pandasを使ってデータを読み込み、前処理を行います。データの前処理には、不要な列の削除、欠損値の処理、カテゴリ変数の数値化などが含まれます。
import pandas as pd
# データの読み込み
data = pd.read_csv('data.csv')
# 不要な列の削除
data.drop(['不要な列名'], axis=1, inplace=True)
# 欠損値の処理
data.fillna(data.mean(), inplace=True)
# カテゴリ変数をダミー変数に変換
data = pd.get_dummies(data, columns=['カテゴリ変数の列名'])特徴量とターゲットの分割
次に、特徴量とターゲット変数を分割します。特徴量はモデルの入力となり、ターゲット変数は予測したい値です。
X = data.drop('ターゲット列名', axis=1)
y = data['ターゲット列名']データの分割
データを訓練セットとテストセットに分割します。これにより、モデルの性能を未知のデータに対して評価できます。
from sklearn.model_selection import train_test_split
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)モデルの訓練
scikit-learnのLinearRegressionクラスを使って、重回帰モデルを訓練します。
from sklearn.linear_model import LinearRegression
# モデルのインスタンス化
model = LinearRegression()
# モデルの訓練
model.fit(X_train, y_train)モデルの評価
訓練されたモデルの性能を評価します。ここでは、テストセットを使用して、モデルの予測精度を確認します。
from sklearn.metrics import mean_squared_error
# テストデータに対する予測
predictions = model.predict(X_test)
# 平均二乗誤差で評価
mse = mean_squared_error(y_test, predictions)
print(f"平均二乗誤差: {mse}")この一連のステップを踏むことで、ライナー君は重回帰分析の冒険に必要なすべてを装備し、データの謎を解き明かす準備が整いました。pandasとscikit-learnの力を借りて、ライナー君はより複雑なデータセットに対しても、精度の高い予測を行うことができるようになります。
実践:新たなるデータの地平へ
冒険は、理論から実践へと進むことで、さらに意味を持ちます。このセクションでは、ライナー君と一緒に、実際の複雑なデータセットを用いて重回帰分析の冒険を体験します。そして、あなた自身の手で、この強力な分析手法を使いこなせるようになりましょう。
ステップ1: データセットを選ぶ
まずは、分析するデータセットを選びます。公開されている多くのデータセットがありますが、例えばKaggleやUCI Machine Learning Repositoryから、興味のあるものを選んでください。不動産価格予測や、消費者行動分析など、重回帰分析を適用できるトピックを選びましょう。
ステップ2: データの前処理
選んだデータセットをダウンロードし、pandasを使ってデータの前処理を行います。欠損値の処理、カテゴリ変数の数値化、不要な列の削除など、データを分析に適した形に整えましょう。
ステップ3: 特徴量の選択
重回帰分析では、複数の独立変数を使って依存変数を予測します。データセットから予測に役立ちそうな特徴量を選び、目的変数と一緒に分析の対象として設定します。
ステップ4: モデルの訓練と評価
scikit-learnを使って重回帰分析モデルを訓練しましょう。訓練セットとテストセットに分割して、モデルの性能を評価します。モデルの予測精度を高めるために、必要に応じて特徴量の選択やハイパーパラメータの調整を行いましょう。ハイパーパラメーターの例:
- 正則化:
RidgeやLasso回帰など、正則化を加えた重回帰分析を使用する場合、正則化の強さを制御するパラメータ(例:alpha)が重要になります。これにより、過学習を防ぎつつモデルの汎用性を高めることができます。 - 特徴量選択: データセットに含まれる特徴量の中で、実際にモデルに含める特徴量を選択することも、間接的なハイパーパラメータ調整の一形態です。不要な特徴量を排除することで、モデルの解釈性を高め、訓練時間を短縮することができます。
- 多項式特徴量: 重回帰分析モデルに多項式特徴量を導入する場合、多項式の次数がハイパーパラメータになります。適切な次数を選択することで、モデルのフィットを改善できますが、高次になりすぎると過学習のリスクが高まります。
これらのハイパーパラメータを調整することで、ライナー君はモデルの予測精度をさらに高め、データの真実に近づくことができます。しかし、これらのパラメータの調整は慎重に行う必要があり、交差検証などの手法を用いて最適な値を見つけ出すことが重要です。
ステップ5: 新たなデータセットで冒険を続ける
一つのデータセットで重回帰分析を体験したら、次は異なるデータセットで同じプロセスを試してみましょう。異なるトピックやデータ構造で分析を行うことで、あなたのデータ分析スキルはさらに向上します。
まとめと未来への一歩
ライナー君と一緒に、重回帰分析の冒険を経て、データの謎を解き明かす旅を進めてきました。この旅を通じて、複数の独立変数を用いて依存変数を予測する重回帰分析の力を体験し、実際にデータセットに適用する方法を学びました。ライナー君が装備した勾配降下法とコスト関数を最適化する技術は、データ分析の基礎として非常に価値があります。
しかし、データサイエンスと機械学習の世界は、重回帰分析だけにとどまりません。無数のテクニックとアルゴリズムが、データから新たな知識を引き出し、予測をより正確にするために開発されています。ここでの学びは、その第一歩に過ぎません。
次なる冒険:ロジスティック回帰分析
ライナー君の次なる冒険は、ロジスティック回帰分析への挑戦です。ロジスティック回帰は、重回帰分析と同様にデータをモデル化する方法ですが、主に分類問題に使用されます。つまり、あるデータポイントが特定のカテゴリに属する確率を予測するために使われます。例えば、メールがスパムであるかどうか、ある病気にかかっているかどうかを予測する場合などに適用されます。
ロジスティック回帰は、出力値を0と1の間に制限するシグモイド関数を使用することが特徴です。これにより、出力を確率として解釈することが可能になります。
あなたの次なる一歩
ライナー君とのこの冒険を通じて、データ分析の基本を学び、実践の重要性を体験しました。しかし、学びの旅はここで終わりではありません。ロジスティック回帰分析のような新たな技術とアルゴリズムに挑戦することで、自分自身のデータ分析スキルをさらに高め、より幅広い問題解決能力を身につけましょう。
この冒険が終わり、次なる冒険が始まります。ロジスティック回帰分析をはじめとする新たなテクニックに挑むことで、機械学習の広大な世界をさらに探求し、データの謎を解き明かす旅を続けましょう。未知のデータセットに潜む洞察と発見が、あなたを待っています。



コメント