【ABC346】競プロのA-C問題を40代サラリーマンがPython解説！初心者にもわかりやすく

AtCoder

こんにちは、こんぶちゃ(茶コーダー)です！

初心者視点から競プロAtCoderのABC346のA問題〜C問題の自身の解答と解答説明をしていきます。

こんな人にオススメしたい
  • 競技プログラミング初心者で、問題の解き方がわからない方
  • AtCoderの公式解説は読んだが、内容が理解できなかった方
  • Pythonでの解法を知りたい方

まだまだ学習の身ですので、最適コードではない部分も多々あるかと思いますが、その部分は同じ学習者として温かい気持ちで応援＆ご助言頂けば嬉しいです。

では早速行ってみましょう！

今回の参加コンテスト(ABC346)

AtCoder Beginner Contest 346

A問題：Adjacent Product

A – Adjacent Product

問題文(要約)

N 個の整数 A1​,A2​,…,AN​ が与えられます。 また、Bi​=Ai​×Ai+1​ (1≤i≤N−1)と定めます。

B1​,B2​,…,BN−1​ をこの順に空白区切りで出力してください。

解答

n=int(input()) # 入力された整数Nを読み込む
A=list(map(int,input().split())) # スペース区切りの整数列をリストAとして読み込む

# 配列Aの隣接する要素の積を計算し、その結果をスペース区切りで出力する
print(*[A[i]*A[i+1] for i in range(n-1)])

考え方）

与えられた問題通りに実装していきます。簡略化のため、内包表記を用いています。

コード詳細

  1. n=int(input())でユーザーから整数Nを入力として受け取ります。これは配列の長さを表します。
  2. A=list(map(int,input().split()))でユーザーからN個の整数をスペース区切りで入力として受け取り、それらを整数のリストAに変換します。
  3. print(*[A[i]*A[i+1] for i in range(n-1)])ではリスト内包表記を使用しています。
    • for i in range(n-1): まず、range(n-1)が生成するシーケンスを用いてループします。n-1は、リストAの要素数より1少ない数です。これは、リストの各要素に対して、その次の要素との演算を行うため、リストの最後の要素には「次の要素」が存在しないためです。
    • A[i]*A[i+1]: リストAの現在の要素（A[i]）とその次の要素（A[i+1]）の積を計算します。これにより、隣接する要素の積からなる新しい値が得られます。
    • [A[i]*A[i+1] for i in range(n-1)]: 上記の計算をリストの最初の要素から最後の一つ前の要素まで行い、その結果から新しいリストを作成します。
    • print(*[...]): 最後に、print関数を使ってこの新しいリストを出力します。リストの前にある*演算子は、リストの要素を展開して、それぞれの要素を個別の引数としてprint関数に渡す役割を果たします。つまり、リストが[1, 2, 3]だとすると、print(1, 2, 3)と呼び出すのと同じ効果があります。これにより、リストの要素がスペース区切りで出力されます。

B問題：Piano

B – Piano

問題

無限に長いピアノの鍵盤があります。 この鍵盤内の連続する区間であって、白鍵 W 個と黒鍵 B 個からなるものは存在しますか？

文字列 wbwbwwbwbwbw を無限に繰り返してできる文字列を S とおきます。

S の部分文字列であって、W 個の w と B 個の b からなるものは存在しますか？

解答

t = 'wbwbwwbwbwbw'  # パターンを表す文字列

w, b = map(int, input().split())  # 白鍵と黒鍵の数を入力から取得

for i in range(len(t)):  # パターン文字列を一文字ずつずらしながら検査
    nw, nb = 0, 0  # 各検査開始時の白鍵(w)と黒鍵(b)の数を0に初期化
    
    for j in range(w+b):  # 指定された合計のキー数だけ繰り返し
        if t[(i+j) % len(t)] == 'w':  # モジュロ演算を使用して循環参照
            nw += 1
        else:
            nb += 1
    
    if nw == w and nb == b:  # 指定された白鍵と黒鍵の数に合致したら
        exit(print('Yes'))  # Yesを出力してプログラムを終了
print('No')  # ループを抜けて合致する部分文字列がなければNoを出力

ポイント）

モジュロ演算（ある数を別の数で割ったときの余りを求める計算：a mod b）を用いることにより、無限（循環）している文字列に対応することができます。上記のコードの t[(i+j) % len(t)] 部分を例をあげて詳しく説明します。

例として、白鍵（w）が2個、黒鍵（b）が3個の場合を考えます。このとき、合計で5個のキーを確認する必要があります。

パターン文字列tは'wbwbwwbwbwbw'で、長さは12です。この文字列を無限に繰り返すと想定して、特定の範囲内で白鍵と黒鍵の指定された数が存在するかを確認します。

for j in range(w+b)ループでは、合計5回の繰り返しを行います。この繰り返しにより、パターン文字列の特定の位置から始めて、連続する5キー（この場合は2つのwと3つのb）をチェックします。

ここで(i+j) % len(t)という計算が重要になります。iはパターン文字列のスタート位置を表し、jはそこからのオフセット（ずれ）を表します。len(t)はパターン文字列の長さ、つまり12です。このモジュロ演算により、パターンの終端に達した後、再びパターンの先頭に戻ることができます。これによって、文字列が無限に繰り返されるかのように扱うことができます。

例えば、i=10（パターン文字列の11文字目からスタート）の場合を考えてみましょう。このとき、jが0から4まで変化します。i+jは10から14までですが、len(t)である12で割った余りを取るため、実際には文字列の位置は10, 11, 0, 1, 2となります。このようにして、パターンの終端を超えた場合でも、自然にパターンの先頭に戻ることができます。

if t[(i+j) % len(t)] == 'w'では、計算された位置のキーが白鍵（w）かどうかをチェックします。白鍵であればnw（白鍵のカウント）を1増やし、そうでなければnb（黒鍵のカウント）を1増やします。最終的に、これらのカウントが指定された白鍵と黒鍵の数と一致するかを確認します。

コード詳細

  1. パターン文字列'wbwbwwbwbwbw'をtに格納します。これは、問題文で与えられた無限に繰り返される文字列の基本単位です。
  2. 入力から白鍵（W）と黒鍵（B）の数を読み込み、それぞれw、bに格納します。
  3. tの各文字に対して、for i in range(len(t))を用いてループを開始します。このループは、パターン文字列の各位置から検査を始めるために使用されます。
  4. 各検査の開始時に、白鍵(nw)と黒鍵(nb)のカウントを0にリセットします。
  5. for j in range(w+b)で、指定された白鍵と黒鍵の合計数だけ繰り返します。この内側のループでは、(i+j) % len(t)を使って、パターン文字列の範囲を超えた場合に循環させることで、無限に繰り返される文字列を模倣します。
  6. if t[(i+j) % len(t)] == 'w'を用いて、現在のキーが白鍵（w）か黒鍵（b）かを判断し、それぞれのカウントを増やします。
  7. もし、ある時点で白鍵のカウントnwがwと等しく、黒鍵のカウントnbがbと等しい場合、'Yes'を出力してプログラムを終了します。
  8. 全ての検査が終了しても条件を満たす部分文字列が見つからない場合、'No'を出力します。

C問題：Σ

C – Σ

問題(要約)

長さ N の正整数列 A=(A1​,A2​,…,AN​) および正整数 K が与えられます。

1 以上 K 以下の整数のうち、A の中に一度も現れないものの総和を求めてください。

解答

# NとKを入力から読み込む
n,k = map(int,input().split())

# Aに含まれる1以上K以下の数を集合として取得
A=set(x for x in set(map(int,input().split())) if x <=k)

# 1からKまでの総和から、Aに含まれる1以上K以下の数の総和を引く
print(((1+k)*k)//2 - sum(A))


解き方）

等差数列の和の公式を用いて、1からKまでの総和を求めるところがポイントになります。

等差数列の初項をa、公差をd、項数をn、n番目の項をl、その和をSn​とします。このとき、等差数列の和の公式は次のように表されます：

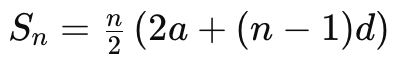
ここでa=1、d=1、そしてn=Kを代入すると、下記のように示されます：

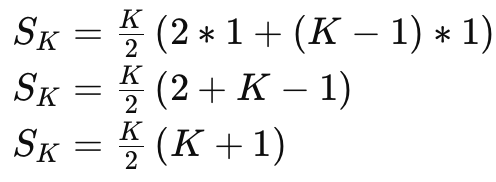
この公式を用いて、１からKまでの総和を求め、リストAに含まれるK以下の数の合計を引けば求める値を算出することができます。

解き方(詳細)：

  1. n,k = map(int,input().split())：ユーザーからNとKの値を一行にスペース区切りで入力されることを想定し、それぞれ整数として読み込みます。
  2. A=set(x for x in set(map(int,input().split())) if x <=k)：
    • input().split()で入力されたN個の整数を読み込み、map(int, ...)で整数のリストに変換します。
    • このリストをset()で集合に変換し、重複を排除します。
    • その後、集合内包表記を使って、1以上K以下の要素のみを新たな集合Aとして抽出します。
  3. print(((1+k)*k)//2 - sum(A))：
    • ((1+k)*k)//2で、1からKまでの整数の総和を計算します。これは等差数列の和の公式を用いています。
    • sum(A)で集合Aに含まれる数の総和を計算します。
    • 最後に、1からKまでの総和から集合Aの総和を引き、Aに一度も現れない数の総和を出力します。

感想

今回は、C問題まで解けました。

A問題は、for文の基本的な問題でしたので、すぐに解くことができました。

B問題の解決にはモジュロ演算が鍵を握っていました。無限に繰り返されるパターンから特定の白鍵(W)と黒鍵(B)の数を含む部分文字列の存在を確認するこの問題は、表面上、無限のデータを扱う必要があるように思えます。しかし、モジュロ演算を活用することで、実際には限定されたパターンを効率的に分析することが可能となりました。

このテクニックにより、問題の本質を見極め、大きなデータセットにも柔軟に対応する方法を学びました。B問題を通じて得たこの洞察は、数の制約が大きな他の問題にも応用できる貴重な学びとなりました。

C問題は、数学的な要素とコーディングが合わさった問題でした。初めは、1からKまでの集合を作って、集合同士の差分を取ることを考えましたが、制約の数が多いため不正解。改めて問題の性質を考えて、等差数列の和の公式が使えることを思いつき、回答に辿り着くことができました。

C問題で素早く(40分以内)で解くことができたため、レーティングが少し上がり520になりました。来週もこのエキサイティングな挑戦を楽しんで続けたいと思います。

それでは、皆さんも競プロライフを楽しんでくださいね！(*＾▽＾)／

コメント

タイトルとURLをコピーしました