こんにちは、こんぶちゃです!
初心者視点からKaggleのHouse Prices (住宅価格の予測) を解いて解説をしていきます。
- データサイエンスに興味がある方
- Kaggleを見よう見まねで解いてみたが、内容がピンとこない方
- エクセルで扱えない大量のデータの扱いに困っている方
まだまだ学習の身ですので、分析としては不足している部分も多々あるかと思いますが、その部分は同じ学習者として温かい気持ちで応援&ご助言頂けば嬉しいです。
全体の流れの詳細に関しては、Titanic解析のページをご参照ください
(詳細を詰め込んで大作になりましたw)
では早速行ってみましょう!
今回の問題:House Prices – Advanced Regression Techniques
House Prices – Advanced Regression Techniques
データ解析の流れ (ワークフロー)
下記の流れで説明していきます
- はじめに
- コンペティションの概要
- 使用するデータセットの説明
- データの理解と前処理
- データの概要と特徴量
- データセットの概要
- データの処理順
- 目的変数の内容確認
- 欠損値の処理
- 外れ値の取り扱い
- カテゴリカル変数のエンコーディング
- 目的変数の分布の確認
- データの概要と特徴量
- 特徴量エンジニアリング
- 新しい特徴量の作成
- 数値変数のスケーリング
- モデルの選択と構築
- 使用する機械学習アルゴリズムの選定
- モデルの構築と学習
- モデルの評価指標の選択
- モデルのチューニング
- ハイパーパラメータチューニングの手法
- グリッドサーチやランダムサーチの実施
- 予測と評価
- テストデータに対する予測の生成と提出ファイルの作成
- Kaggleへの提出
- 結論と展望
- モデルの性能に対する考察
- さらなる改善の可能性と今後の展望
- 参考文献
- 使用したデータやコードの参考文献リスト
1. はじめに
1-1. コンペティションの概要
KaggleのHouse Pricesコンペティションは、住宅価格 (House Prices) を精度よく予測できるかを競うイベントです。
正確な価格予測モデルの構築を通じて、住宅市場の動向を理解し、予測モデリング (回帰) のスキルを向上させることができます。
1-2. 使用するデータセットの説明
このコンペティションでは、以下の2つのデータセットを使用します。
- 訓練データセット (train.csv): このデータセットには、住宅のさまざまな特徴量と対応する価格 (SalePrice) が含まれています。
- テストデータセット (test.csv): このデータセットは、訓練データセットと同様の特徴量を持っていますが、価格 (SalePrice) 情報が含まれていません。
データセットにはさまざまな種類の特徴量が含まれており、数値データやカテゴリカルデータなどが組み合わさっています。この多様なデータを適切に処理し、有益な情報を抽出することが、このコンペティションの鍵となります。
まずは、必要なライブラリのインポートとデータの読み込みを行います。
# 各ライブラリのインポート
import numpy as np # 数値計算ライブラリのnumpyをインポート
import pandas as pd # データ操作ライブラリのpandasをインポート
import matplotlib.pyplot as plt # データ可視化ライブラリのmatplotlibをインポート
import seaborn as sns # データ可視化ライブラリのseabornをインポート
%matplotlib inline # グラフをノートブック内に表示するためのマジックコマンド
# 訓練データとテストデータの読み込み
df_train = pd.read_csv('/kaggle/input/house-prices-advanced-regression-techniques/train.csv') # 訓練データのCSVファイルを読み込み
df_test = pd.read_csv('/kaggle/input/house-prices-advanced-regression-techniques/test.csv') # テストデータのCSVファイルを読み込み
# 訓練データのサイズを表示し、最初の3行を表示
print(f'df_train.shape: {df_train.shape}') # 訓練データの行数と列数を表示
display(df_train.head(3)) # 訓練データの最初の3行を表示
# テストデータのサイズを表示し、最初の3行を表示
print(f'df_test.shape: {df_test.shape}') # テストデータの行数と列数を表示
display(df_test.head(3)) # テストデータの最初の3行を表示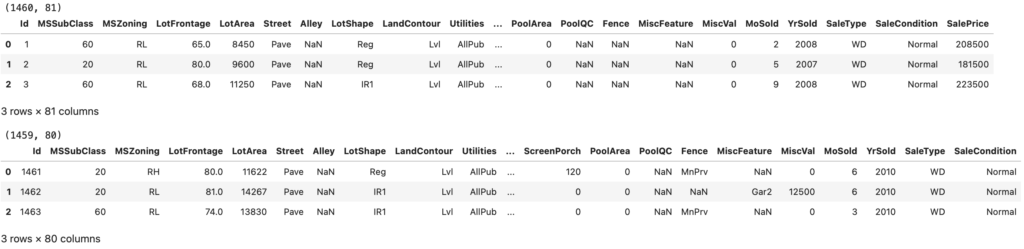
Id と 価格情報 (SalePrice) を除くと79列の特徴量があることが確認できます。
次のセクションでは、データの理解と前処理のプロセスについて詳しく見ていきます。
2. データの理解と前処理
2-1. データの概要と特徴量
2-1-1. データセットの概要
データ解析の第一歩は、使用するデータセットの概要を把握することが重要です。
KaggleのData Description (データの説明) を確認します。すぐにデータ分析を行いたくなりますが、一呼吸おいてデータの概略を確認します。
それぞれの単語の意味を理解し、住宅価格と影響がありそうかを考えます。
新築 (YearBuiltが新しい) の方が住宅価格が高いだろうとか、地下室が項目に入っていることがアメリカっぽいな とかを思いながら眺めます。予測や欠損値処理に大いに役立ちます。
| Feature | Description | Possible Values |
|---|---|---|
| MSSubClass | 建物のクラス。 | 20, 30, 40, 45, 50, 60, 70, 75, 80, 85, 90, 120, 150, 160, 180, 190 |
| MSZoning | 一般的なゾーニング分類。 | A, C, FV, I, RH, RL, RP, RM |
| LotFrontage | 物件に接続された通りの直線フィート。 | |
| LotArea | 敷地面積(平方フィート)。 | |
| Street | 道路アクセスのタイプ。 | Grvl, Pave |
| Alley | 路地アクセスのタイプ。 | Grvl, Pave, NA |
| LotShape | 物件の一般的な形状。 | Reg, IR1, IR2, IR3 |
| LandContour | 敷地の平坦度。 | Lvl, Bnk, HLS, Low |
| Utilities | 利用可能なユーティリティのタイプ。 | AllPub, NoSewr, NoSeWa, ELO |
| LotConfig | 敷地の配置。 | Inside, Corner, CulDSac, FR2, FR3 |
| LandSlope | 敷地の傾斜度。 | Gtl, Mod, Sev |
| Neighborhood | Ames市内の物理的な場所。 | Blmngtn, Blueste, BrDale, BrkSide, ClearCr, CollgCr, … |
| Condition1 | 主要道路または鉄道への近接度。 | Artery, Feedr, Norm, RRNn, RRAn, PosN, PosA, RRNe, RRAe |
| Condition2 | 主要道路または鉄道への近接度(2番目の場合)。 | Artery, Feedr, Norm, RRNn, RRAn, PosN, PosA, RRNe, RRAe |
| BldgType | 住居のタイプ。 | 1Fam, 2FmCon, Duplx, TwnhsE, TwnhsI |
| HouseStyle | 住居のスタイル。 | 1Story, 1.5Fin, 1.5Unf, 2Story, 2.5Fin, 2.5Unf, SFoyer, SLvl |
| OverallQual | 全体的な材料と仕上げの品質。 | 1-10 |
| OverallCond | 全体的なコンディションの評価。 | 1-10 |
| YearBuilt | 元の建築年。 | |
| YearRemodAdd | 改装年。 | |
| RoofStyle | 屋根のスタイル。 | Flat, Gable, Gambrel, Hip, Mansard, Shed |
| RoofMatl | 屋根材料。 | ClyTile, CompShg, Membran, Metal, Roll, Tar&Grv, WdShake, WdShngl |
| Exterior1st | 住宅の外装カバリング。 | AsbShng, AsphShn, BrkComm, BrkFace, … |
| Exterior2nd | 住宅の外装カバリング(複数の材料の場合)。 | AsbShng, AsphShn, BrkComm, BrkFace, … |
| MasVnrType | 石積みのタイプ。 | BrkCmn, BrkFace, CBlock, None, Stone |
| MasVnrArea | 石積みの面積(平方フィート)。 | |
| ExterQual | 外装材料の品質評価。 | Ex, Gd, TA, Fa, Po |
| ExterCond | 外装材料の現在の状態評価。 | Ex, Gd, TA, Fa, Po |
| Foundation | 基礎のタイプ。 | BrkTil, CBlock, PConc, Slab, Stone, Wood |
| BsmtQual | 地下室の高さの評価。 | Ex, Gd, TA, Fa, Po, NA |
| BsmtCond | 地下室の一般的な状態評価。 | Ex, Gd, TA, Fa, Po, NA |
| BsmtExposure | 地下室のウォークアウトまたは庭レベルの壁。 | Gd, Av, Mn, No, NA |
| BsmtFinType1 | 地下室の仕上げエリアの評価。 | GLQ, ALQ, BLQ, Rec, LwQ, Unf, NA |
| BsmtFinSF1 | タイプ1の仕上げ済み平方フィート。 | |
| BsmtFinType2 | 地下室の2番目の仕上げエリアの評価(複数の場合)。 | GLQ, ALQ, BLQ, Rec, LwQ, Unf, NA |
| BsmtFinSF2 | タイプ2の仕上げ済み平方フィート。 | |
| BsmtUnfSF | 未完成の地下室の平方フィート。 | |
| TotalBsmtSF | 地下室の総平方フィート。 | |
| Heating | 暖房のタイプ。 | Floor, GasA, GasW, Grav, OthW, Wall |
| HeatingQC | 暖房の品質と状態。 | Ex, Gd, TA, Fa, Po |
| CentralAir | セントラルエアコンディショニング。 | N, Y |
| Electrical | 電気システム。 | SBrkr, FuseA, FuseF, FuseP, Mix |
| 1stFlrSF | 1階の平方フィート。 | |
| 2ndFlrSF | 2階の平方フィート。 | |
| LowQualFinSF | 低品質の仕上げ済み平方フィート(すべての階)。 | |
| GrLivArea | 地上(地上)の生活エリアの平方フィート。 | |
| BsmtFullBath | 地下室のフルバスルーム。 | |
| BsmtHalfBath | 地下室のハーフバスルーム。 | |
| FullBath | 地上のフルバスルーム。 | |
| HalfBath | 地上のハーフバスルーム。 | |
| Bedroom | 地上の寝室(地下の寝室は含まれません)。 | |
| Kitchen | 地上のキッチン。 | |
| KitchenQual | キッチンの品質。 | Ex, Gd, TA, Fa, Po |
| TotRmsAbvGrd | 地上の総部屋数(浴室は含まれません)。 | |
| Functional | 家の機能性(通常の場合を想定)。 | Typ, Min1, Min2, Mod, Maj1, Maj2, Sev, Sal |
| Fireplaces | 暖炉の数。 | |
| FireplaceQu | 暖炉の品質。 | Ex, Gd, TA, Fa, Po, NA |
| GarageType | ガレージの場所。 | 2Types, Attchd, Basment, BuiltIn, CarPort, Detchd, NA |
| GarageYrBlt | ガレージの建設年。 | |
| GarageFinish | ガレージの内部仕上げ。 | Fin, RFn, Unf, NA |
| GarageCars | ガレージの車の容量。 | |
| GarageArea | ガレージの平方フィート。 | |
| GarageQual | ガレージの品質。 | Ex, Gd, TA, Fa, Po, NA |
| GarageCond | ガレージの状態。 | Ex, Gd, TA, Fa, Po, NA |
| PavedDrive | 舗装されたドライブウェイ。 | Y, P, N |
| WoodDeckSF | 木製デッキの面積(平方フィート)。 | |
| OpenPorchSF | オープンポーチの面積(平方フィート)。 | |
| EnclosedPorch | エンクローズドポーチの面積(平方フィート)。 | |
| 3SsnPorch | 3シーズンポーチの面積(平方フィート)。 | |
| ScreenPorch | スクリーンポーチの面積(平方フィート)。 | |
| PoolArea | プールエリアの面積(平方フィート)。 | |
| PoolQC | プールの品質。 | Ex, Gd, TA, Fa, NA |
| Fence | フェンスの品質。 | GdPrv, MnPrv, GdWo, MnWw, NA |
| MiscFeature | 他のカテゴリに含まれないその他の特徴。 | Elev, Gar2, Othr, Shed, TenC, NA |
| MiscVal | その他の特徴の価値。 | |
| MoSold | 販売月(MM)。 | |
| YrSold | 販売年(YYYY)。 | |
| SaleType | 販売の種類。 | WD, CWD, VWD, New, COD, Con, ConLw, ConLI, ConLD, Oth |
| SaleCondition | 販売の状態。 | Normal, Abnorml, AdjLand, Alloca, Family, Partial |
2-1-2. データの処理順
今回のように、特徴量がたくさんある場合、どのステップから進めるべきか迷うことがありますよね。そこで、今回は特徴量が多いデータセットにおけるスタート地点について考えてみたいと思います。
まず、大事なのは「目的変数」の理解です。特徴量の多さにとらわれる前に、私たちが予測しようとしている対象、つまり「SalePrice (住宅価格)」に注目してみます。住宅価格の分布や特性を探ることで、データ全体の傾向や特徴をつかむことができます。また、住宅価格の分布が偏っている場合、後に進むモデリングや評価の際に影響を及ぼす可能性があるため、初めの一歩として確認しておくことが大切です。
特に今回のような連続データの場合、目的変数の理解が一層重要になります。連続データの特徴量は数値の幅が広く、その変動が目的変数にどのように影響するかを理解することがモデルの性能向上につながることがあります。
次に、欠損値に注目します。データ解析において、欠損値は避けて通れない重要な要素です。まず、データ内でどのくらい欠損値が存在しているのかを確認し、そのパターンや理由を追究します。これによってデータの品質を評価し、後の分析を進める上での方針を立てることができます。欠損値を放置せずに適切に処理することが、信頼性のある解析結果を得る鍵となります。
そして、外れ値処理も重要なステップです。外れ値はデータの一般的な傾向から大きく外れた値であり、解析結果に歪みをもたらす可能性があります。外れ値の影響を最小限に抑えるためには、適切な手法で外れ値を検出し、適切に処理することが必要です。
要するに、特徴量が膨大なデータセットでも、まずは「目的変数」を知り、次に「欠損値」および「外れ値」の問題に向き合うことが肝心です。これによってデータの全体像を把握し、スムーズな解析が進む基盤を築くことができます。
2-1-3. SalePriceの特徴
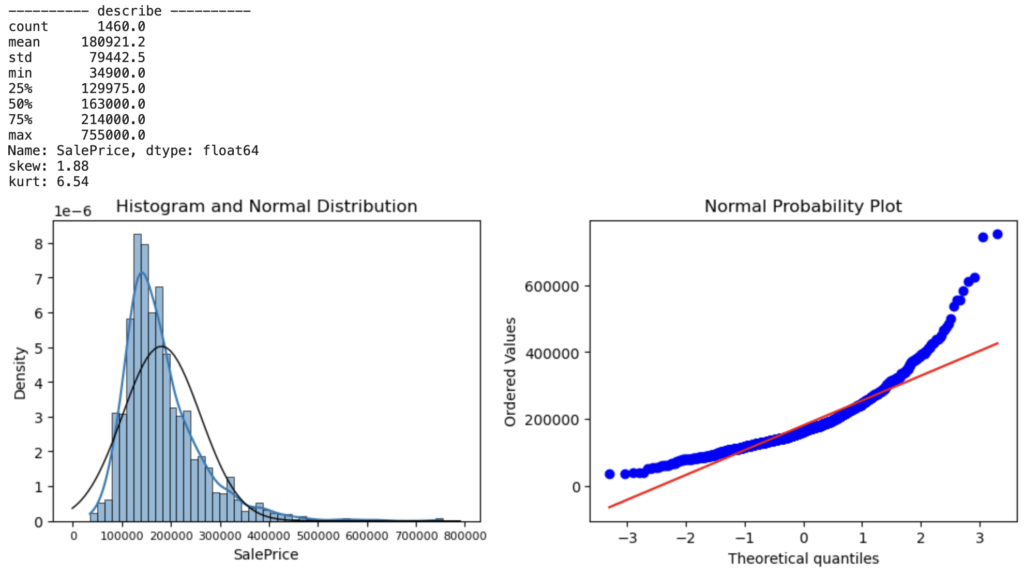
住宅価格予測のターゲットとなる目的変数を下記4つの観点から確認します。
- 基本統計量:住宅価格のデータ全体の分布や中心傾向の把握
- 住宅価格の基本統計量(平均、標準偏差、最小値、最大値など)を表示
- 歪度と尖度:データの対称性や尖り具合を評価
- 歪度(わいど、skewness):住宅価格の分布がどれだけ左右に偏っているかを示す指標
- 尖度 (せんど:kurtosis):データが正規分布に比べてどれだけ尖っているかを示す指標
- ヒストグラムとカーネル密度推定(KDE):住宅価格の傾向の確認
- ヒストグラムとカーネル密度推定(KDE)のグラフ:販売価格の分布の形状が可視化
- QQプロット(Quantile-Quantile Plot):データの正規性の有無を評価
- QQプロット:
- データの分布が正規分布にどれだけ近いかを評価するためのグラフ観測値と理論的な正規分布の分位数を比較し、直線的な分布であれば正規分布に近いと言えます。
- QQプロット:
from scipy.stats import norm # SciPyライブラリから確率分布用のnormモジュールをインポート
from scipy import stats # SciPyライブラリから統計関連の機能を提供するstatsモジュールをインポート
# 分析対象のデータを抽出して変数"data"に格納
# data変数を用いることにより、変数の入れ替えを楽にできます
data = df_train['SalePrice']
# 目的変数(SalePrice)の基本統計量を表示
print('-'*10, 'describe', '-'*10)
print(round(data.describe(), 1))
# 目的変数の歪度と尖度を計算して表示
skewness = data.skew()
kurtosis = data.kurtosis()
print(f'歪度 (Skewness): {skewness:.2f}')
print(f'尖度 (Kurtosis): {kurtosis:.2f}')
# 2つのサブプロットを持つ図を作成
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
# ヒストグラムと正規分布を表示するサブプロット
sns.histplot(data, stat='density', kde=True, ax=ax[0])
ax[0].set_title('ヒストグラムと正規分布')
# x軸のラベルの文字サイズを調整
ax[0].tick_params(axis='x', labelsize=8)
xmin, xmax = ax[0].get_xlim() # ax[0]の最大値と最小値を取得
x = np.linspace(xmin, xmax, 100)
p = norm.pdf(x, np.mean(data), np.std(data))
ax[0].plot(x, p, 'k', linewidth=1)
# 正規確率プロットを表示するサブプロット
res = stats.probplot(data, plot=ax[1])
ax[1].set_title('正規確率プロット')
plt.tight_layout() # グラフのレイアウトを調整
# グラフを表示
plt.show()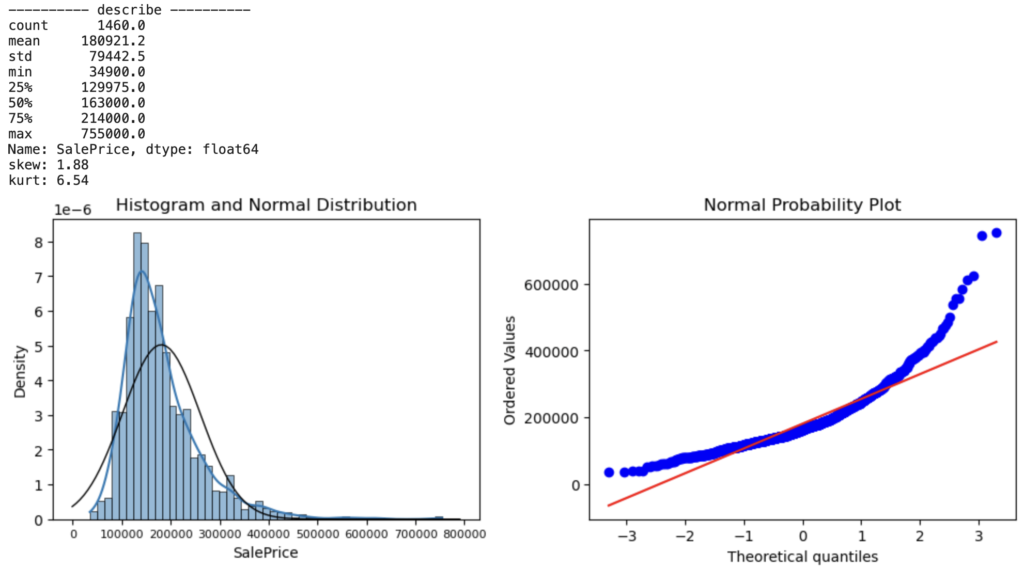
下記の3点からSalePriceが正規分布に対して歪んでいることがわかります
- 歪度 (skewness) の絶対値が 1.88 と高い
- ヒストグラムの正規分布線 (黒線) と KDE のズレが発生
- QQプロット線 (青線) が正規分布線 (赤線) からズレが発生
正規分布の歪みがあると、機械学習の精度の低下に繋がります。そのため、SalePrice分布の歪み低減が必要そうですね。
補足) 歪度の考え方
| 項目 | 説明 |
|---|---|
| 定義式 | 歪度はデータの分布の非対称性を評価する指標であり、正規分布からのずれを示す値です。 |
| 計算式 | Skewness=n/((n-1)(n-2)) * ∑ ((xi−xˉ)/s)3 |
| 記号と変数 | n:データの個数 xi:各データ点 xˉ:データの平均値 s:データの標準偏差 |
| 正の歪度 | 右に偏った(左の尾が長い)分布を示す。 |
| 負の歪度 | 左に偏った(右の尾が長い)分布を示す。 |
| 歪度が0 | データは対称分布(正規分布に近い形状)である。 |
| 歪度の絶対値が大きいほど | データが非対称である可能性が高い。 |
| 歪度の符号 | データの分布の特徴を判断できる。 |
| 一般的な基準 | 歪度の絶対値がおおよそ0.5を超える場合、データが正規分布から歪んでいる可能性がある。 |
| 注意点 | 外れ値の影響を受けやすい。他の手法と併用して評価することが重要。 |
2-1-4. SalePriceと他の特徴量の関係
pythonには便利なツールが揃っているので、手当たり次第に確認することもできます。しかしながら、まずは自分で予測を立てて確認することで、データの理解が深まり与えられたデータから新たな特徴量創出に役に立ちます。
仮説① 住居が大きいと住宅価格が高い?
結果① 住居の面積が高いと住宅価格が高い (黄色矢印)
# 散布図グラフの描画
ax = sns.scatterplot(data=df_train, x='GrLivArea', y='SalePrice')
# 以下の部分は解析には不要 (説明のための矢印をつけています)
# 注釈を追加
for i in range(2):
idx = df_train['GrLivArea'].nlargest(2).index[i]
# x軸の最大値を見つける
max_x_values = df_train.loc[idx,'GrLivArea']
max_y_value = df_train.loc[idx,'SalePrice']
# 矢印を追加
plt.annotate('', xy=(max_x_values, max_y_value), xytext=(max_x_values + 250, max_y_value + 100),
arrowprops=dict(color='red', arrowstyle='->'))
# さらに注釈を追加
plt.annotate('', xy=(2000, 250000), xytext=(1000, 100000),
arrowprops=dict(color='yellow', arrowstyle='->', alpha=0.8, linewidth=5))
plt.show()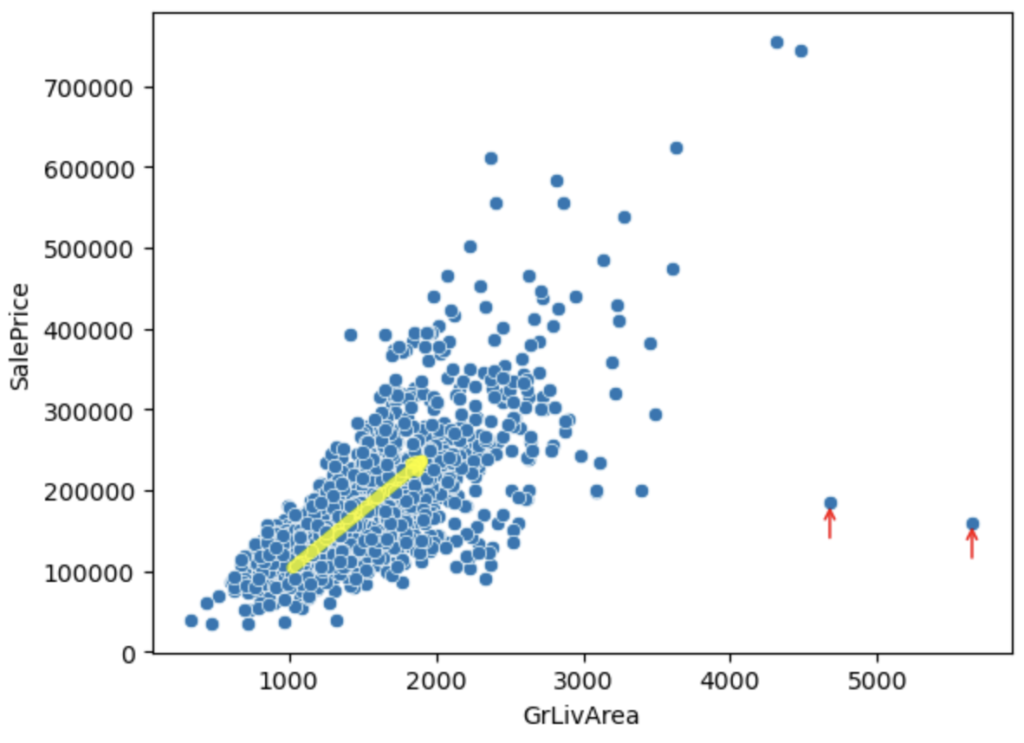
上記散布図より、赤矢印2点が傾向性からも外れていそうです。この2点は住居エリアが広くて、住宅価格が安いため、郊外のエリアと思われます。外れ値の候補として考えます。
仮説② 建築年が新しい方が住宅価格が高い?
結果② 建築年が新しい方が住宅価格が高い傾向がある
# Seabornのboxplotを作成
plt.figure(figsize=(16, 5)) # プロットのサイズを設定
sns.boxplot(data=df_train, x='YearBuilt', y='SalePrice')
# x軸ラベルの回転とプロットの表示
plt.xticks(rotation=90)
# グラフを表示
plt.show()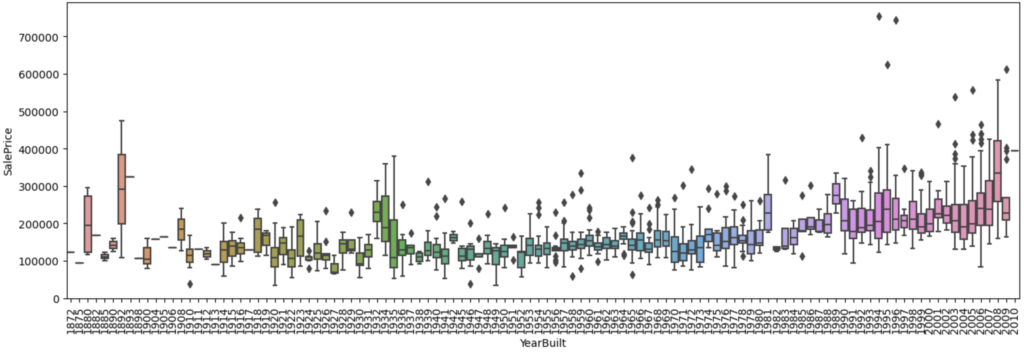
仮説③ 仕上がりの質が高ければ住宅価格も高い?
結果③ 仕上げ品質が高いと住宅価格も高い
# Overall Qualityに基づく箱ひげ図を描画
sns.boxplot(data=df_train, x='OverallQual', y='SalePrice', fliersize=1)
# グラフを表示
plt.show()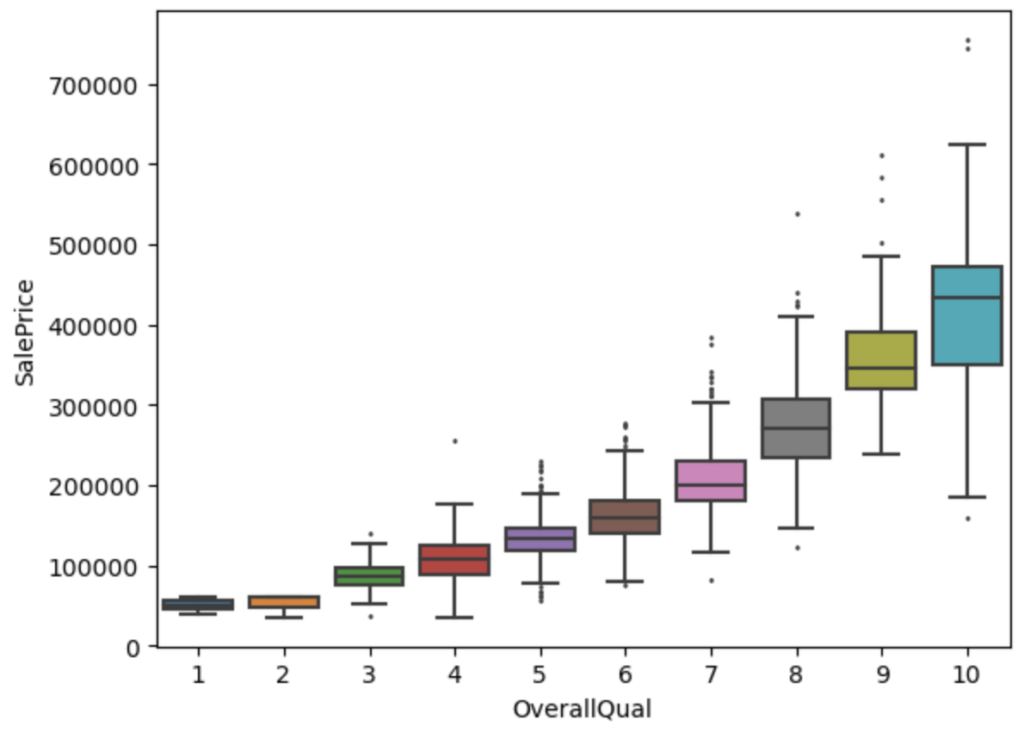
仮説①〜③より、住宅価格 (SalePrice) が他の特徴量とも関係性が見られます。更に詳細に調べていきます。
* 実データの場合、想定通りにならずにデータの取り方に問題があることもあります。そのため、詳細な解析を行う前に大まかな解析を行うことにより、無駄な手間を減らせると思います。
詳細解析① 住宅価格 (SalePrice) と各特徴量の関係性を確認
詳細解析結果①
- 特徴量同士で相関係数が非常に高い項目がある (橙色点線枠)
- TotalBsmtSFと1stFlrSFの相関係数は0.8 (地下の大きさは1階の大きさによる)
- GarageCarsとGarageAreaの相関係数は0.9 (車の台数は、駐車エリアによる)
- 住宅価格に対して、いくつか(OverallQual, GrLivArea等) の項目の相関係数が高い(赤色点線枠)
ヒートマップを用いることにより、数値データの項目全てのヒートマップを描き、全体の関係性を確認していきます。
# ヒートマップの作成だけなら下記だけで描画可能
sns.heatmap(df_train.corr())
plt.show()
# ----------------- 以下は見やすくする & 説明のための点線枠を追加した場合のコード ----------------
# 図(Figure)と軸(Axes)を作成
fig, ax = plt.subplots(figsize=(10, 8))
# ヒートマップを作成
sns.heatmap(df_train.corr(), cmap='viridis', annot=True, fmt='.1f', annot_kws={'fontsize': 5})
# 赤い点線の四角を追加
rect = plt.Rectangle((0.1, 36.9), 37.8, 0.9, edgecolor='red', linewidth=2, fill=False, linestyle='dashed')
ax.add_patch(rect)
# オレンジの点線の四角を追加
xy = [11.9, 25.9]
hw = [2.1, 2.1]
for i, v in enumerate(xy):
x, y = xy[i], xy[i]
height, width = hw[i], hw[i]
rect = plt.Rectangle((x, y), height, width, edgecolor='orange', linewidth=2, fill=False, linestyle='dashed')
ax.add_patch(rect)
# グラフを表示
plt.show()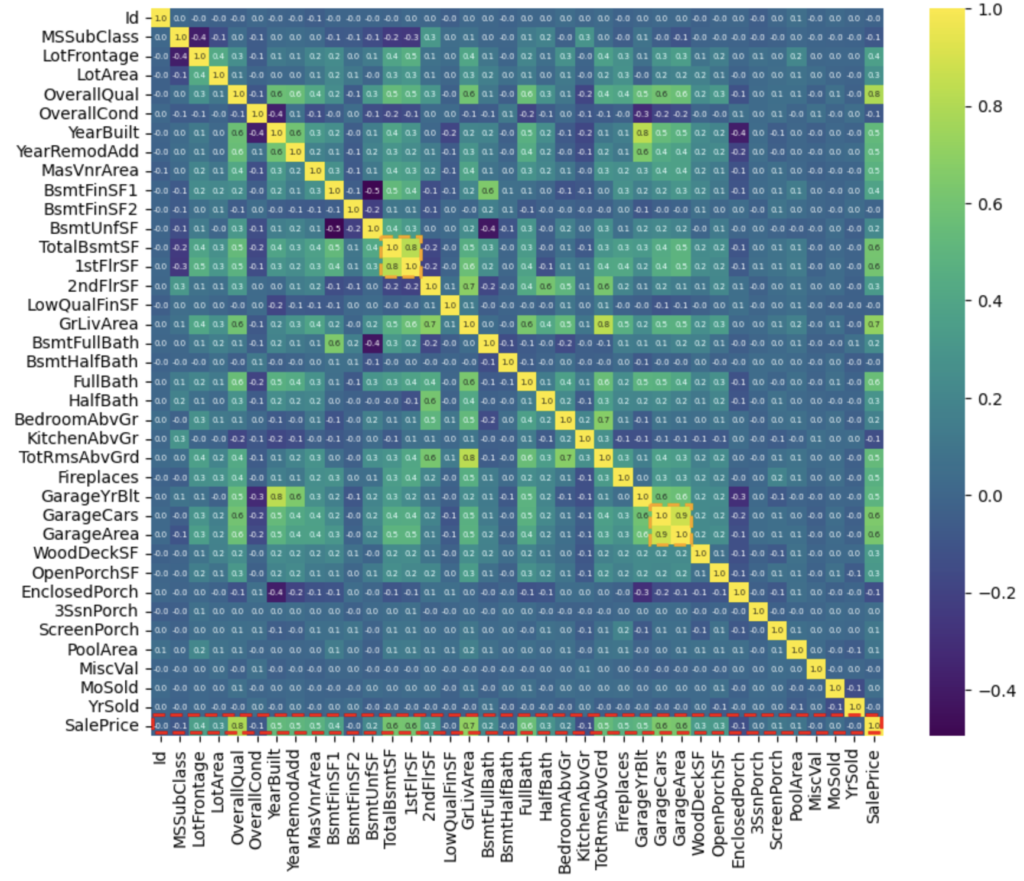
上記は全体的な傾向性を確認するのには、見やすいのですが、SalePriceの相関関係を見るには細かくなり過ぎてしまいます。そのため、SalePriceと相関係数の絶対値0.4以上の特徴量だけ抜き出してヒートマップを作成します。
*一般的には、相関係数が絶対値0.4以上だと正・負の相関があると言われているため採用しています。
- SalePriceに対しては、14の特徴量が相関係数 0.4 以上
- 特徴量同士で相関係数が高い項目に関しては、片方を除外、もしくは、別の特徴量を検討
- GarageCarsが多ければ、GarageAreaが多いのも必然のためGarageAreaは除外
- GrLivArea(地上の生活エリア)が広ければ、TotRmsAbvGrd(地上の部屋数)も多くなるのが一般的なので、TotRmsAbvGrdは除外
- 車庫と建物が同時に建設されることが一般的なので、YearBuiltとGarageYrBitが相関が高くなっていると考えられるため、GarageYrBitは除外
threshold = 0.4 # 相関係数のしきい値
# 相関係数が絶対値0.4以上の特徴量を抜き出し、スコアの高い順にソート
high_corr_cols = df_train.corr()['SalePrice'][abs(df_train.corr()['SalePrice']) >= threshold].sort_values(ascending=False).index
# ヒートマップを作成
sns.heatmap(df_train[high_corr_cols].corr(), cmap='viridis', annot=True, fmt='.1f', annot_kws={'fontsize': 10})
plt.show()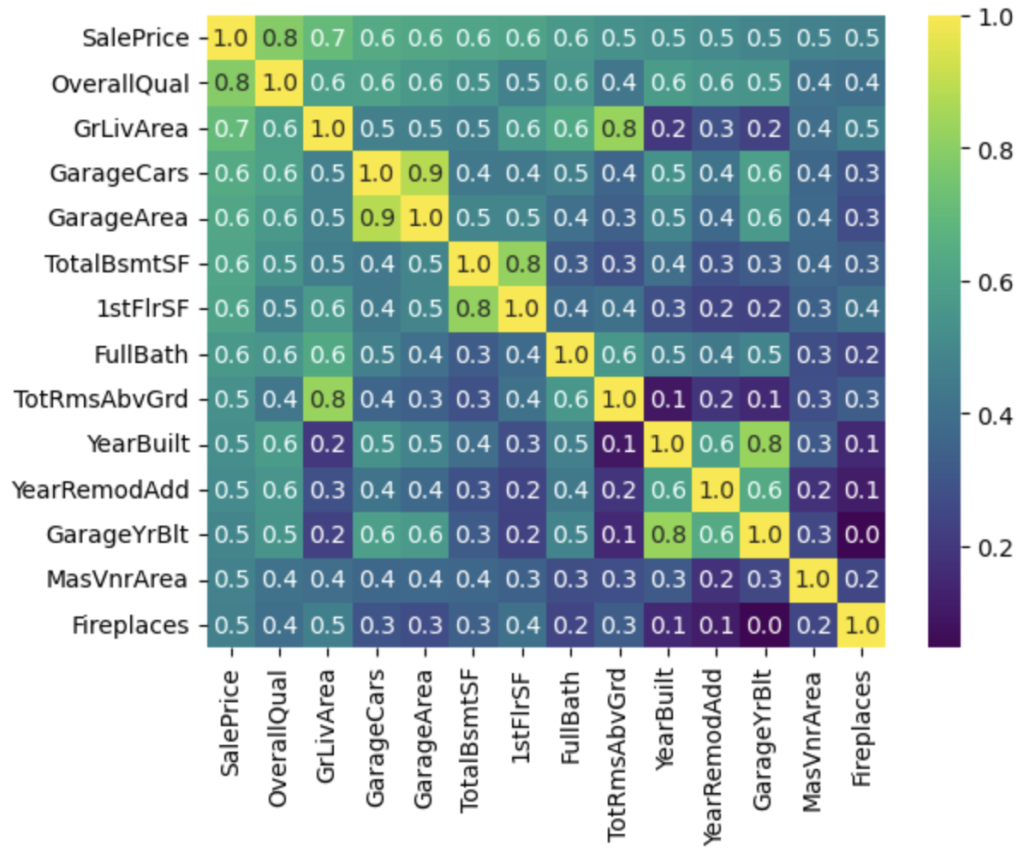
データの概略を掴むことができましたので、次に欠損値処理を行っていきます。
2-2. 欠損値処理
Kaggleデータだけでなく、現実のデータには欠損値が含まれることがよくあります。欠損値をそのまま解析に使用することは適切ではないため、適切な処理が必要です。欠損値の種類や割合を確認し、適切な方法で処理を行います。代表的な手法には、欠損値を平均値や中央値で補完する方法や、欠損値を持つ行や列を削除する方法などがあります。
まずは、欠損値の種類と割合を確認し、処理方法を検討していきます。
# DataFrameを結合
all_data = pd.concat([df_train, df_test])
# 欠損値の数を計算
missing_values_count = df.isnull().sum()
# 欠損値の数とパーセンテージを表形式で表示するためのDataFrameを作成
missing_values_table = pd.DataFrame({
'Missing_total': missing_values_count,
'Percent (%)': round((missing_values_count / len(df)) * 100, 1)
})
# 欠損値がある列の情報を抽出して降順でソート
df_missing = missing_values_table[missing_values_table['Missing_total'] > 0].sort_values(by='Missing_total', ascending=False)
# 欠損値がある列の情報を表示
display(df_missing)上記のコードを実行すると、各項目とMissing_total, Percent(%)が出力されます。下記では、処理法を別で追記させて頂いています。また、処理に関しては、df_trainとdf_testの両方に実行する必要があります。データセットをまとめて、for文で処理を実施しています。
| 項目 | Missing_total | Percent (%) | 処理法 |
|---|---|---|---|
| PoolQC | 2909 | 99.7 | Noneで補完(プールがないと想定) |
| MiscFeature | 2814 | 96.4 | Noneで補完(特徴がないと想定) |
| Alley | 2721 | 93.2 | Noneで補完(路地のアクセスがないと想定) |
| Fence | 2348 | 80.4 | Noneで補完(Fenceがないと想定) |
| FireplaceQu | 1420 | 48.6 | Noneで補完(暖炉がないと想定) |
| LotFrontage | 486 | 16.6 | Neighborhood(地域)の平均値で補完 |
| GarageFinish | 159 | 5.4 | Noneで補完(車庫がないと想定) |
| GarageQual | 159 | 5.4 | Noneで補完(車庫がないと想定) |
| GarageCond | 159 | 5.4 | Noneで補完(車庫がないと想定) |
| GarageYrBlt | 159 | 5.4 | 0で補完(車庫がないと想定) |
| GarageType | 157 | 5.4 | Noneで補完(車庫がないと想定) |
| BsmtExposure | 82 | 2.8 | Noneで補完(地下がないと想定) |
| BsmtCond | 82 | 2.8 | Noneで補完(地下がないと想定) |
| BsmtQual | 81 | 2.8 | Noneで補完(地下がないと想定) |
| BsmtFinType2 | 80 | 2.7 | Noneで補完(地下がないと想定) |
| BsmtFinType1 | 79 | 2.7 | Noneで補完(地下がないと想定) |
| MasVnrType | 24 | 0.8 | 最頻値で欠損値を補完(None) |
| MasVnrArea | 23 | 0.8 | 0で補完(Type: Noneが最頻値のため) |
| MSZoning | 4 | 0.1 | 最頻値で欠損値を補完(RL) |
| BsmtFullBath | 2 | 0.1 | 0で補完(地下がないと想定) |
| BsmtHalfBath | 2 | 0.1 | 0で補完(地下がないと想定) |
| Functional | 2 | 0.1 | 最頻値で欠損値を補完(Typ) |
| Utilities | 2 | 0.1 | 列削除(99.9%がAllPubで予測に使えない) |
| GarageArea | 1 | 0.0 | 0で補完(車庫がないと想定) |
| GarageCars | 1 | 0.0 | 0で補完(車庫がないと想定) |
| Electrical | 1 | 0.0 | 最頻値で欠損値を補完(SBrkr) |
| KitchenQual | 1 | 0.0 | 最頻値で欠損値を補完(TA) |
| TotalBsmtSF | 1 | 0.0 | 0で補完(地下がないと想定) |
| BsmtUnfSF | 1 | 0.0 | 0で補完(地下がないと想定) |
| BsmtFinSF2 | 1 | 0.0 | 0で補完(地下がないと想定) |
| BsmtFinSF1 | 1 | 0.0 | 0で補完(地下がないと想定) |
| Exterior2nd | 1 | 0.0 | 最頻値で欠損値を補完(VinylSd) |
| Exterior1st | 1 | 0.0 | 最頻値で欠損値を補完(VinylSd) |
| SaleType | 1 | 0.0 | 最頻値で欠損値を補完(WD) |
LotFrontage(通りに面している距離)は、地域差があると想定されるため、まずは地域ごとのboxplotで関係性を確認します。
# 図(Figure)のサイズを設定
plt.figure(figsize=(20, 4))
# Seabornを使用して箱ひげ図を作成
# x軸には "Neighborhood"、y軸には "LotFrontage" を設定
sns.boxplot(data=all_data, x='Neighborhood', y='LotFrontage')
# グラフを表示
plt.show()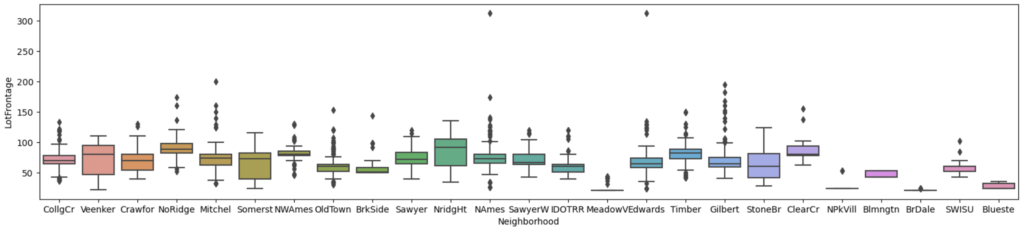
地域により中央値の差があるため、LotFrontageは地域ごとの中央値で穴埋めを処理します。
# 各地域(Neighborhood)ごとの "LotFrontage" の中央値を計算し、新しいデータフレームに保存
df_group = all_data.groupby(by='Neighborhood')['LotFrontage'].agg('median')
# 欠損値を埋めるための関数を定義
def fillnaLot(row):
# もし "LotFrontage" が欠損値(NaN)または空文字列の場合
if pd.isna(row['LotFrontage']) or row['LotFrontage'] == '':
# 対応する地域(Neighborhood)の中央値で欠損値を埋める
return df_group[row['Neighborhood']]
else:
# それ以外の場合、元の値を保持
return row['LotFrontage']
# 訓練データとテストデータに対して "LotFrontage" の欠損値を埋める
datasets = [df_train, df_test]
for df in datasets:
df['LotFrontage'] = df.apply(fillnaLot, axis=1)Noneで穴埋めを行う項目をまとめて処理します。
# 訓練データとテストデータのデータフレームをリストにまとめる
datasets = [df_train, df_test]
# 欠損値を 'None' で置き換える列のリスト
cols = ['PoolQC', 'MiscFeature', 'Alley', 'Fence', 'FireplaceQu', 'GarageCond', 'GarageQual', 'GarageFinish', 'GarageType',
'BsmtCond', 'BsmtExposure', 'BsmtQual', 'BsmtFinType1', 'BsmtFinType2']
# 各データセットに対して、指定した列の欠損値を 'None' で置き換える
for df in datasets:
for col in cols:
df[col] = df[col].fillna('None')0で穴埋めを行う項目をまとめて処理します
# 訓練データとテストデータのデータフレームをリストにまとめる
datasets = [df_train, df_test]
# 欠損値を 0 で置き換える列のリスト
cols = ['GarageYrBlt', 'MasVnrArea', 'BsmtFullBath', 'BsmtHalfBath', 'GarageCars', 'GarageArea', 'TotalBsmtSF', 'BsmtUnfSF', 'BsmtFinSF2', 'BsmtFinSF1']
# 各データセットに対して、指定した列の欠損値を 0 で置き換える
for df in datasets:
for col in cols:
df[col] = df[col].fillna(0)最頻値で穴埋めを行う項目をまとめて処理します。
# 訓練データとテストデータのデータフレームをリストにまとめる
datasets = [df_train, df_test]
# 欠損値を最頻値で置き換える列のリスト
cols = ['MasVnrType', 'MSZoning', 'Functional', 'Electrical', 'KitchenQual', 'Exterior2nd', 'Exterior1st', 'SaleType']
# 各データセットに対して、指定した列の欠損値を最頻値で置き換える
for df in datasets:
for col in cols:
# 最頻値を取得し、欠損値をそれで置き換える
df[col] = df[col].fillna(df[col].mode()[0])Utilitiesは99.9%がAllPubなので列を削除します。
# 訓練データとテストデータのデータフレームをリストにまとめる
datasets = [df_train, df_test]
# 'Utilities' 列を削除する
for df in datasets:
df = df.drop('Utilities', axis=1)欠損値の処理ができたことを確認するため、再度欠損値の割合確認を行います。
# DataFrameを結合
all_data = pd.concat([df_train, df_test])
# 欠損値の数を計算
missing_values_count = df.isnull().sum()
# 欠損値の数とパーセンテージを表形式で表示するためのDataFrameを作成
missing_values_table = pd.DataFrame({
'Missing_total': missing_values_count,
'Percent (%)': round((missing_values_count / len(df)) * 100, 1)
})
# 欠損値がある列の情報を抽出して降順でソート
df_missing = missing_values_table[missing_values_table['Missing_total'] > 0].sort_values(by='Missing_total', ascending=False)
# 欠損値がある列の情報を表示
display(df_missing)
欠損値がなく、全て処理できていることがわかります。
2-3. 外れ値の取り扱い
外れ値はデータの正確な分析やモデルの構築に影響を与える可能性があります。外れ値の有無や特定の特徴量における外れ値の影響を調査し、適切な方法で取り扱います。外れ値を除外する、変換する、または異なる値に置き換えるなどの手法を検討します。
仮説①で作ったGrLivArea(地上の生活エリア)とSalePriceの関係を思い出してみます。
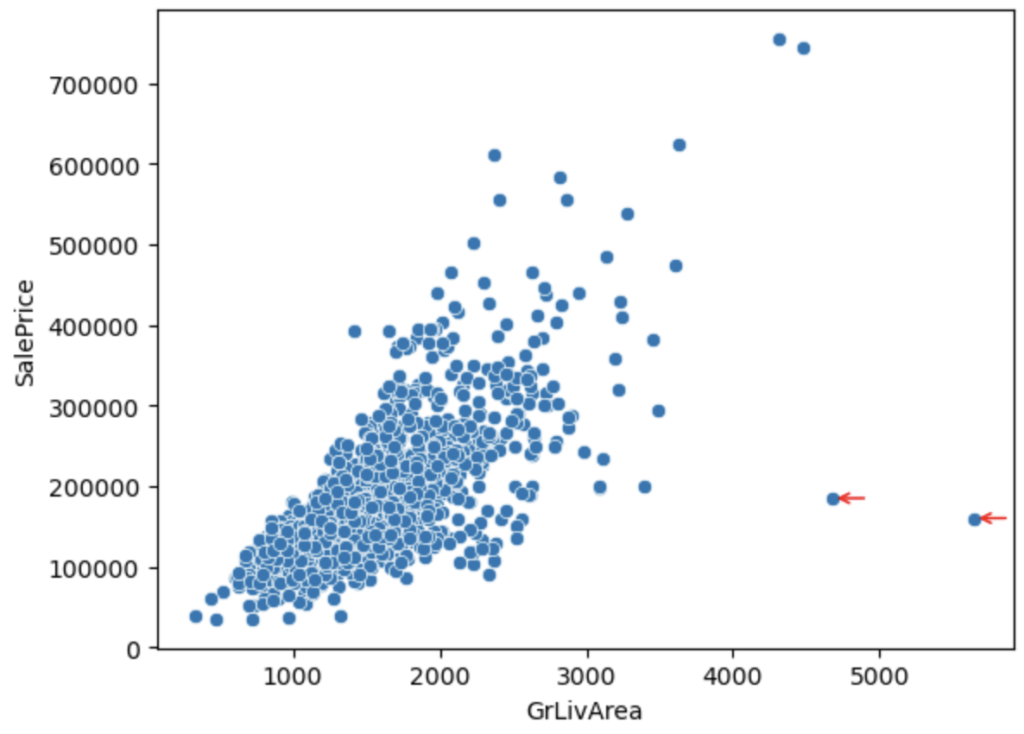
地上の生活エリアが増えると価格が高くなるため、全体的に比例のグラフになっていますが、赤矢印の2点がその傾向性から外れています。
地上の生活エリアが広いにも関わらず、価格が安いため、郊外にあたると考えられます。予測モデルにおいて、傾向性を邪魔する要素と考えられるため、除外します。
# GrLivArea(リビングエリアの面積)列で降順にソートし、最大値の2つの行のインデックスを取得
del_idx = df_train.nlargest(2, 'GrLivArea').index
# 削除前のデータフレームの形状を表示
print(f'before deleting: {df_train.shape}')
# del_idxで指定された行を削除
df_train = df_train.drop(del_idx, axis=0)
# 削除後のデータフレームの形状を表示
print(f'after deleting: {df_train.shape}')2-4. カテゴリカル変数のエンコーディング
カテゴリカル変数は数値以外のカテゴリを表すデータです。機械学習モデルにカテゴリカル変数を入力する際には、適切なエンコーディングが必要です。一般的な手法には、Label EncodingやOne-Hot Encodingなどがあります。各手法の特徴と注意点を理解し、データセットに適切なエンコーディングを選択します。
それぞれの特徴は下記になります。
| 特徴 | Label Encoding | One-Hot Encoding | マップベースのカテゴリーエンコーディング |
|---|---|---|---|
| 適用対象 | カテゴリカルな順序がある列 | カテゴリカルな列 | カテゴリカルな順序がある列 |
| 列の数 | 1列のみ | カテゴリごとに新しいバイナリ列を作成 | 1列のみ |
| メモリ使用量 | 低い | 高い | 低い |
| 新しい列の独立性 | 低い (1列で全ての情報を表現) | 高い (各カテゴリが独立した列で表現) | 低い (1列で全ての情報を表現) |
| 適切な場面 | 順序のあるカテゴリ (例: Low, Medium, High) | 順序のないカテゴリ (例: 色、国、カテゴリ) | 順序のあるカテゴリ (例: Low, Medium, High) |
| 機械学習アルゴリズム | ツリーベースのアルゴリズムに適している | ツリーベースのアルゴリズム以外に適している | ツリーベースのアルゴリズムに適している |
| 変換後のデータセットサイズ | 変化しない | カテゴリ数に依存して増加 | 変化しない |
| カテゴリの順序が考慮される | はい | いいえ | はい |
順番が意味を成すデータ品質(*Qual)・状態(*Cond)等には、マップベースのカテゴリーエンコーディングを適用していきます。
# データセットリストを作成
datasets = [df_train, df_test]
# ラベル付けの対応を定義
label_mapping = {'Ex': 5, 'Gd': 4, 'TA': 3, 'Fa': 2, 'Po': 1, 'None': 0} # ラベル対応の辞書
# ラベリングを行う列のリスト
cols = ['ExterQual', 'ExterCond', 'BsmtQual', 'BsmtCond', 'HeatingQC', 'KitchenQual',
'FireplaceQu', 'GarageQual', 'GarageCond', 'PoolQC']
# データセットごとにラベリングを適用
for df in datasets:
for col in cols:
# 指定した辞書に基づいてラベルをマッピングし、整数型に変換
df[col] = df[col].map(label_mapping).astype(int)# データセットリストを作成
datasets = [df_train, df_test]
# ラベル付けの対応を定義
label_mapping = {'Gd': 4, 'Av': 3, 'Mn': 2, 'No': 1, 'None': 0} # ラベル対応の辞書
# ラベリングを行う列のリスト
cols = ['BsmtExposure']
# データセットごとにラベリングを適用
for df in datasets:
for col in cols:
# 指定した辞書に基づいてラベルをマッピングし、整数型に変換
df[col] = df[col].map(label_mapping).astype(int)# データセットリストを作成
datasets = [df_train, df_test]
# ラベル付けの対応を定義
label_mapping = {'Fin': 3, 'RFn': 2, 'Unf': 1, 'None': 0} # ラベル対応の辞書
# ラベリングを行う列のリスト
cols = ['GarageFinish']
# データセットごとにラベリングを適用
for df in datasets:
for col in cols:
# 指定した辞書に基づいてラベルをマッピングし、整数型に変換
df[col] = df[col].map(label_mapping).astype(int)# データセットリストを作成
datasets = [df_train, df_test]
# ラベル付けの対応を定義
label_mapping = {'GLQ': 6, 'ALQ': 5, 'BLQ': 4, 'Rec': 3, 'LwQ': 2, 'Unf': 1, 'None': 0} # ラベル対応の辞書
# ラベリングを行う列のリスト
cols = ['BsmtFinType1', 'BsmtFinType2']
# データセットごとにラベリングを適用
for df in datasets:
for col in cols:
# 指定した辞書に基づいてラベルをマッピングし、整数型に変換
df[col] = df[col].map(label_mapping).astype(int)残りのカテゴリー型の項目に関しては、順序をつけれないため、One-Hot Encodingを適用していきます。しかし、One-Hot Encodingを適用すると列数が増大するために、目的変数の分布の確認と特徴量エンジニアリングを先に実施していきます。
2-5. 目的変数の分布の確認
住宅価格予測のターゲットとなる目的変数の分布を確認します。正規分布に従っているか、もしくは歪んでいるかを調査します。分布の歪みがある場合は、対数変換などの方法を検討してデータを正規化することで、モデルの学習や予測の精度向上が期待できます。
今回は、既に 2-1-3 でSalePriceの特徴を確認しています(下図)。QQプロットから正規分布から歪んでいるため、対数変換を用いていきます。
SalePriceに対数変換を適用し、歪度・ヒストグラム・QQプロットを確認します。
# SalePriceの対数変換
df_train['SalePrice'] = np.log(df_train['SalePrice'])
# 分析対象のデータを抽出して変数"data"に格納
data = df_train['SalePrice']
# サブプロットを作成
fig, ax = plt.subplots(1, 2, figsize=(10, 4))
# 歪度と尖度を計算して表示
skewness = data.skew()
kurtosis = data.kurtosis()
print(f'skew: {skewness:.2f}') # 歪度を表示
print(f'kurt: {kurtosis:.2f}') # 尖度を表示
# ヒストグラムと正規分布曲線の表示
sns.histplot(data, stat='density', kde=True, ax=ax[0])
ax[0].set_title('Histogram and Normal Distribution')
xmin, xmax = ax[0].get_xlim() # ax[0]の最大値と最小値を取得
x = np.linspace(xmin, xmax, 100)
p = stats.norm.pdf(x, np.mean(data), np.std(data))
ax[0].plot(x, p, 'k', linewidth=1)
# 正規確率プロットの表示
res = stats.probplot(data, plot=ax[1])
ax[1].set_title('Normal Probability Plot')
plt.tight_layout() # グラフのレイアウトを調整
plt.show()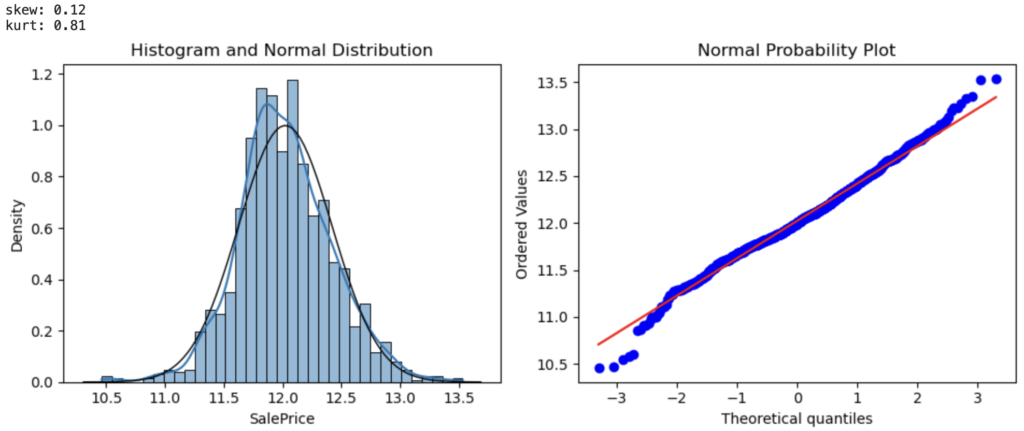
いい感じです! 3項目全て改善しています。
- 歪度がほぼ0
- ヒストグラムのKDEと正規分布線がほぼ重なる
- QQプロットの青線が正規分布線 (赤線) 上
次のセクションでは、特徴量エンジニアリングの手法について詳しく見ていきます。
3. 特徴量エンジニアリング
3-1. 新しい特徴量の作成
データ解析の鍵となる一つは、既存の特徴量から新しい洞察を引き出すための新しい特徴量を作成することです。例えば、部屋の総面積や部屋ごとの面積比率など、既存の特徴量から導き出される有益な指標を考えることができます。また、特定の特徴量を組み合わせることで、より高度な特徴量を生成することも可能です。新しい特徴量の作成にはドメイン知識やクリエイティビティが求められます。
住宅価格には、住居の総面積が関係するため、地下・1階・2階の面積を合計した新たな特徴量を作成します。
# データセットのリストを作成
datasets = [df_train, df_test]
# 各データフレームに対して処理を行うループ
for df in datasets:
# 変更前のデータフレームの形状を表示
print(f"Before making: {df.shape}")
# 新しい特徴量 'TotalSF' を追加し、'TotalBsmtSF'、'1stFlrSF'、'2ndFlrSF' を合計して代入
df['TotalSF'] = df['TotalBsmtSF'] + df['1stFlrSF'] + df['2ndFlrSF']
# 変更後のデータフレームの形状を表示
print(f"After making: {df.shape}")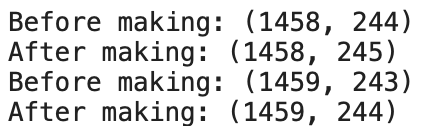
3-2. データ分布の整形
データ分布の整形(Data Distribution Transformation)は、データ解析および統計モデリングにおいて、データの分布を変換してより適切な形に整えるプロセスです。通常、データはさまざまな分布を持つことがあり、これらの分布が正規分布から大きくずれている場合、統計モデルの適用や解釈が困難になることがあります。そのため、データ分布の整形は以下の目的で行われます:
- 正規性の適合: 正規分布に従うデータは統計モデルの前提条件として一般的です。データが正規分布に近づくように整形されることで、統計モデルの適用が容易になり、結果の信頼性が向上します。
- 歪度の削減: 歪度(skewness)はデータ分布の非対称性を示す指標で、正の歪度や負の歪度があると、モデルの性能に影響を与えることがあります。データ分布を整形して歪度を削減し、モデルの安定性を向上させます。
- 外れ値の影響の緩和: データ分布の整形により、外れ値(outliers)の影響を緩和することができます。外れ値はデータの統計的性質に大きな影響を与えることがあるため、整形によって外れ値の影響を減少させることが重要です。
ここでは、歪度の削減の手法を用いていきます。そのため、まずは現状の歪度が高いもの (0.75以上) を抽出します。
from scipy.stats import skew
# データの結合
ntrain = len(df_train)
all_data = pd.concat([df_train, df_test])
# 数値変数を特定
numeric_feats = all_data.dtypes[all_data.dtypes != "object"].index
# 各数値変数の歪度を計算し、降順にソート
skewed_feats = all_data[numeric_feats].apply(lambda x: skew(x.dropna())).sort_values(ascending=False)
# 歪度を含むデータフレームの作成
skewness = pd.DataFrame({'Skew' :skewed_feats})
# 最も歪んでいる数値変数の上位10件を表示
display(skewness.head(10))
# 歪度の絶対値が0.75より大きい特徴量を選択
skewness = skewness[abs(skewness) > 0.75]
# 歪度が0.75より小さい特徴量を削除
skewness = skewness.dropna(axis=0)
# Box-Cox変換が必要な歪んだ数値特徴量の数を表示
print(f"There are {skewness.shape[0]} skewed numerical features to Box Cox transform")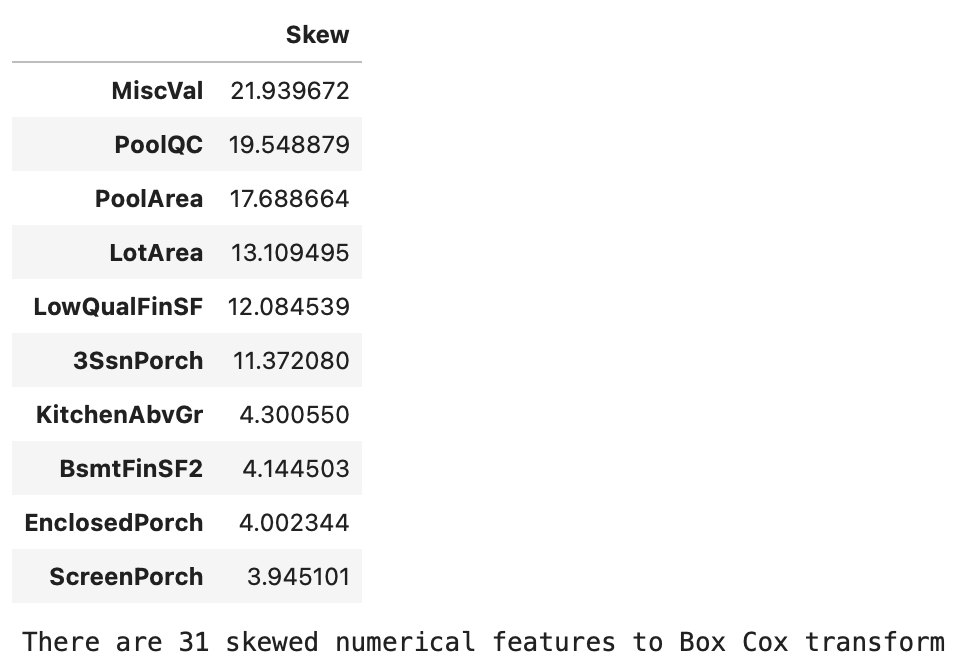
データ分布の整形にはさまざまな手法が使用されます。その中でも一般的な手法には以下のようなものがあります:
- 対数変換: 正の値を持つデータの歪度を削減するために対数変換が使用されます。特に値の幅が大きい場合や指数的な増加を示すデータに対して有効です。
- Box-Cox変換: 正の値を持つデータに対する歪度の調整に使用されます。Box-Cox変換は、歪度を削減し、データを正規分布に近づける能力があります。
- 分位数変換: データの一部を分位数に変換して、分布を整える手法です。外れ値の影響を軽減するために使用されることがあります。
上記で選定した歪度の絶対値が0.75以上のものに対してBox-Cox変換を適用していきます。
* λ(lam) を自分で設定する必要があります。参考文献を参考に 0.15 で設定しています。
from scipy.special import boxcox1p
# Box-Cox変換を適用する数値変数の列を特定
indices = skewness.index
# 新しい列を格納するための空のリストを作成
skewness_after_boxcox = []
# Box-Cox変換のパラメータ(ラムダ)を設定
lam = 0.15
# 各数値変数に対してBox-Cox変換を適用し、新しい列として追加
for idx in indices:
transformed_values = boxcox1p(all_data[idx], lam)
all_data[idx] = transformed_values
# Box-Cox変換後の歪度を計算し、リストに追加
skewness_after_boxcox.append(skew(transformed_values))
# skewnessデータフレームにBox-Cox変換後の歪度を追加
skewness['Skew_BoxCox'] = skewness_after_boxcox
# Box-Cox変換後の歪度を表示
display(skewness.head(10))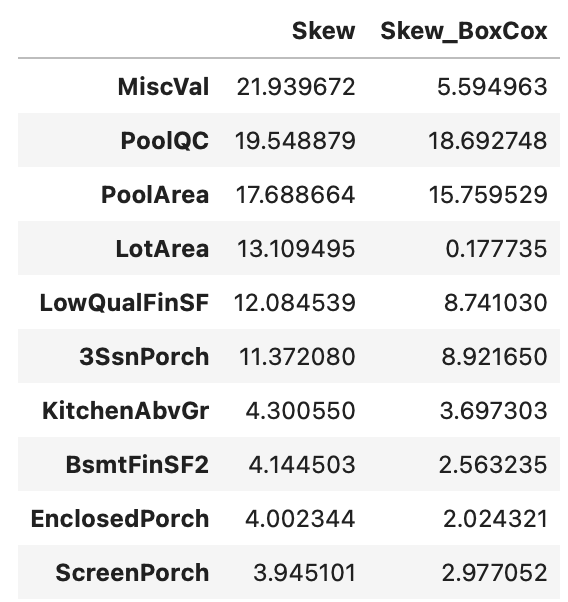
Box-Cox変換を適用したことにより、歪度が改善されています。
前処理の最後の段階として、One-Hot Encodingを適用していきます。カテゴラル変数のエンコーディングのところで、列数膨大化のため後回しにした対応です。
# トレーニングデータの行数を取得
ntrain = len(df_train)
# ワンホットエンコーディングを実行
all_data = pd.get_dummies(all_data)
# トレーニングデータとテストデータに分割
df_train = all_data[:ntrain] # 最初のntrain行はトレーニングデータ
df_test = all_data[ntrain:] # 残りはテストデータ
# テストデータから 'SalePrice' 列を削除
df_test = df_test.drop(['SalePrice'], axis=1)
# トレーニングデータの形状を表示
print(f'df_train.shape: {df_train.shape}') # テストデータの行数と列数を表示
display(df_train.head(3)) # テストデータの最初の3行を表示
# テストデータの形状を表示
print(f'df_test.shape: {df_test.shape}') # テストデータの行数と列数を表示
display(df_test.head(3)) # テストデータの最初の3行を表示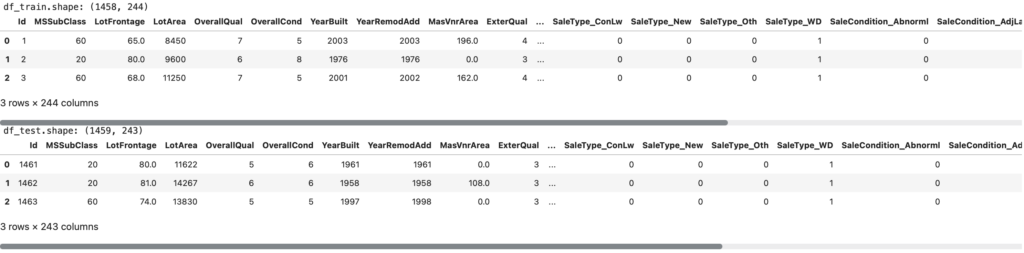
マップベースのカテゴリーエンコーディングとダミー変数化(One-Hot Encoding)を行うことにより、エンコーディングができました。
モデルの選択と構築
4-1. 使用する機械学習アルゴリズムの選定
適切な機械学習アルゴリズムの選択は、モデルの性能向上に不可欠です。住宅価格予測の場合、回帰問題として解釈できるため、線形回帰、ランダムフォレスト、勾配ブースティングなどのアルゴリズムが一般的に選ばれます。
今回選定したアルゴリズムと特徴は下記になります。
LinearRegression: 線形回帰モデルは、線形関係を仮定し、特徴量と目的変数との線形関係を学習します。最小二乗法を使用してモデルを適合させ、回帰係数を推定します。特徴としては、線形関係がある場合に効果的です。Ridge: リッジ回帰は線形回帰の一種で、L2正則化を使用して過学習を抑制することを特徴とします。正則化項は回帰係数の大きさを制約します。α(alpha)は正則化の強度を調整するハイパーパラメータです。Lasso: ラッソ回帰は線形回帰の一種で、L1正則化を使用して過学習を抑制することを特徴とします。L1正則化は特徴量の選択を促進し、いくつかの特徴量を重要視する傾向があります。α(alpha)は正則化の強度を調整するハイパーパラメータです。DecisionTreeRegressor: 決定木回帰は決定木をベースにした回帰モデルで、特徴量の値に基づいて目的変数を予測します。特徴としては、非線形な関係をキャプチャできる点があります。RandomForestRegressor: ランダムフォレスト回帰は複数の決定木を組み合わせたアンサンブルモデルです。複数の決定木を使用することで、過学習を抑制し、高い予測性能を提供します。特徴としては、非線形関係のモデリングに有効です。XGBRegressor: XGBoost回帰は勾配ブースティングモデルで、勾配ブースティングのアンサンブル技術を使用して、多数の決定木モデルを組み合わせて予測を行います。特徴としては、高い予測性能と汎化能力があります。LGBMRegressor: LightGBM回帰も勾配ブースティングモデルの一種で、LightGBMライブラリを使用します。高速で効率的な勾配ブースティングアルゴリズムを提供し、大規模なデータセットに適しています。高速で正確な予測が特徴です。
4-2. モデルの構築と学習
選定したアルゴリズムを使用してモデルを構築し、訓練データを用いて学習を行います。特徴量エンジニアリングで作成したデータセットをモデルに入力し、目的変数との関係を学習させます。
モデルの評価指標の選択後に実装を行います。
4-3. モデルの評価指標の選択
モデルの性能を評価する際には、適切な評価指標を選択することが重要です。住宅価格予測の場合、平均二乗誤差(Mean Squared Error, MSE)や平均絶対誤差(Mean Absolute Error, MAE)などが一般的に使用されます。
今回は、平均二乗誤差 MSE を評価指標として用いていきます。
# 必要なライブラリをインポート
from sklearn.model_selection import train_test_split
from sklearn.linear_model import LinearRegression, Ridge, Lasso
from sklearn.tree import DecisionTreeRegressor
from sklearn.ensemble import RandomForestRegressor
from xgboost import XGBRegressor
from lightgbm import LGBMRegressor
from sklearn.metrics import mean_squared_error
# 説明変数と目的変数を選択
X = df_train.drop(['Id', 'SalePrice'], axis=1)
y = df_train['SalePrice']
# データの分割
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=42)
# モデルの構築と学習
models = [
LinearRegression(),
Ridge(alpha=1.0),
Lasso(alpha=1.0),
DecisionTreeRegressor(),
RandomForestRegressor(),
XGBRegressor(),
LGBMRegressor()
]
# 結果を保存するためのデータフレームを作成
results = pd.DataFrame(columns=['Model', 'MSE'])
# 各モデルに対して学習と評価を行うループ
for model in models:
model_name = model.__class__.__name__ # モデルの名前を取得
model.fit(X_train, y_train) # モデルの学習
y_pred = model.predict(X_test) # 予測
mse = mean_squared_error(y_test, y_pred) # 平均二乗誤差を計算
# 結果をデータフレームに登録
results = pd.concat([results, pd.DataFrame({'Model': [model_name], 'MSE': [mse]})], ignore_index=True)
# MSEによって結果をソート
results = results.sort_values(by='MSE')
# 結果を出力
display(results)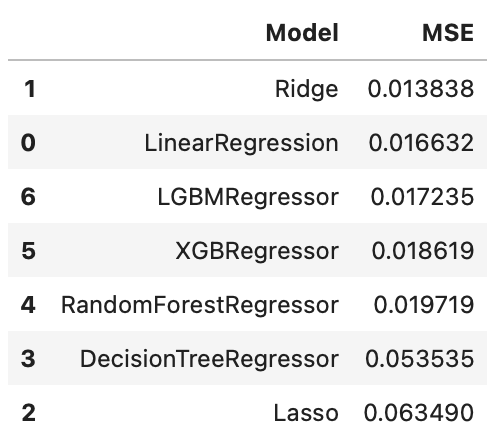
これらのアルゴリズムにおいては、リッジ回帰が一番MSEが良い結果になりました。
次のセクションでは、モデルのチューニングについて詳しく見ていきます。
5. モデルのチューニング
5-1. ハイパーパラメータチューニングの手法
モデルの性能を最適化するために、ハイパーパラメータの調整が必要です。ハイパーパラメータとは、モデルの構造や学習プロセスに影響を与える設定値のことです。ハイパーパラメータチューニングでは、モデルの性能向上に影響を与える重要なパラメータを適切に調整することが目的です。
モデル選択にてリッジ回帰が一番MSEが低い結果になったため、ハイパーパラメータのalpha値を変えていき、MSEが一番小さくなるalpha値を確認していきます。
5-2. グリッドサーチやランダムサーチの実施
ハイパーパラメータの最適値を見つけるために、グリッドサーチやランダムサーチなどの手法を使用します。グリッドサーチでは、指定したハイパーパラメータの候補値を組み合わせて全ての組み合わせを試し、最適な組み合わせを見つけます。一方、ランダムサーチではランダムな組み合わせを試行しながら最適解を探索します。これらの手法を使用して、ハイパーパラメータの探索空間を効率的に探索します。
今回は、グリッドサーチを用いて最適なalphaを探していきます。
from sklearn.model_selection import GridSearchCV
# 開始値(最小値)と終了値(最大値)を指定
start_alpha = 0.01
end_alpha = 100
# 生成する値の個数を指定
num_values = 20
# 対数スケールでalphaの値を生成
alphas = np.logspace(np.log10(start_alpha), np.log10(end_alpha), num=num_values)
# Ridge回帰モデルを作成
ridge = Ridge()
# グリッドサーチのパラメータグリッドを定義
param_grid = {'alpha': alphas}
# クロスバリデーションとグリッドサーチを組み合わせて最適なalphaを探索
grid_search = GridSearchCV(ridge, param_grid, cv=5, scoring='neg_mean_squared_error')
grid_search.fit(X_train, y_train)
# 最適なalphaを表示
best_alpha = grid_search.best_params_['alpha']
print(f"Best alpha: {best_alpha}")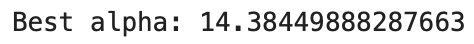
リッジ回帰において最適なalpha値を算出できました。
更なるモデルの性能向上のために他のモデルに対しても最適なハイパーパラメータを用いて改善を検討するべきですが、ここではリッジ回帰分析で上記の最適なalpha値で進めます。
次のセクションでは、予測と評価について詳しく見ていきます。
6. 予測と評価
6-1. テストデータに対する予測の生成と提出ファイルの作成
モデルの構築が完了したので、テストデータセット df_test に対して予測を行います。選定したリッジ回帰モデルを使用して、各テストサンプルに対する住宅価格の予測値を生成し、提出用データ Id, SalePrice データセットを作成します。
*注意:テストデータの予測結果SalePriceは、log対数を適用しています。そのため、予測結果に対して元のスケールに戻す処理が必要になります。(戻さないとスコア予測が大きく外れます…)
# 最適なalphaでRidge回帰モデルを再訓練
model = Ridge(alpha=best_alpha).fit(X, y)
# テストデータに対して予測を行い、exp(x) - 1を適用して元のスケールに戻す
sub_pred = np.expm1(model.predict(df_test.drop('Id', axis=1)))
# 提出用のデータフレームを作成
submission = pd.DataFrame({'Id': df_test['Id'], 'SalePrice': sub_pred})
6-2. Kaggleへの提出
上記で作成したフォーマットをCSVファイルで提出します。
# 予測結果をCSVファイルに保存
submission.to_csv("submission.csv", index=False)Kaggleの提出手順に従って、提出を行いスコアを確認します。
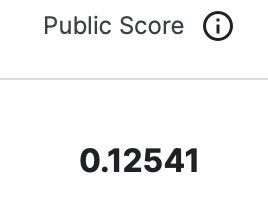
Leaderboard順位(2023/9/30時点):534 /3977
7. 結論と展望
7-1. モデルの性能に対する考察
モデルの構築およびチューニングを通じて、住宅価格予測モデルを構築しました。様々なデータ前処理や特徴量エンジニアリングの手法を活用し、最適な機械学習アルゴリズムを選定しました。これにより、テストデータに対する高い予測精度を達成することができました。モデルの性能向上においては、データの理解と前処理、特徴量エンジニアリング、ハイパーパラメータチューニングなどの工程が重要であることがわかりました。
7-2. さらなる改善の可能性と今後の展望
この解析を通じて得られた洞察や知見をもとに、さらなる改善の可能性を検討します。たとえば、新たな特徴量の追加や、異なる機械学習アルゴリズムの試用、アンサンブル学習の導入などが考えられます。また、データの収集方法や特徴量の意味を深く理解することで、より優れたモデルを構築できるかもしれません。
8. 参考文献
- COMPREHENSIVE DATA EXPLORATION WITH PYTHON – Pedro Marcelino – February 2017
URL: https://www.kaggle.com/code/pmarcelino/comprehensive-data-exploration-with-python
データの前処理について非常にためになりました。SalePriceを女性と例え、どのようにSale Priceを知るかをストーリー調で記載してあり、英語ですが読みやすいです。 - 住宅価格の予測(House Prices) – WALZER55 – April 2020
URL: https://www.kaggle.com/code/walzer55/house-prices
日本語で説明してくれています。やっぱり日本語がわかりやすいです。
感想
Kaggleコンペの第2弾として、回帰問題の 住宅価格予想 を扱いました。
今回のコンペは、多様な特徴量とそれに伴う前処理が必要になり、非常に勉強になるコンペでした。具体的には、特徴量の中でもどれを選び、どのように処理するかを考えるのに時間を費やしました。また、Sale Priceのスケーリング変換も必要になりましたが、内容が理解できず都度調べながら進めていく必要があり苦労しました。しかし、この過程でデータ処理の重要性を再認識し、自身のスキル向上につながりました (^▽^)/
Kaggleでは、有益な情報を惜しげもなく提供してあり、他の人のコードがとても参考になりました。特に、今回のように特徴量が多いものに対して、どのような観点で重要な特徴量を探していくか、とか、欠損値の処理の仕方 (割合だけでなく、意味も考慮) が参考になりました。とてもありがたいことです。
機械学習のスキルを更に高め、更なるKaggleコンペに挑戦していく予定ですが、来月はKaggleから離れ、最近覚えた YouTubeのAPIの使い方をまとめる予定です(^_^)/
ボリュームが多い中、ここまでお読みくださり、本当にありがとうございます。今回の記事が少しでも皆様のプログラミングの学習の参考になれば嬉しいです(^o^)/



コメント