こんにちは、こんぶちゃ(茶コーダー)です!
初心者視点から競プロAtCoderのABC353のA問題〜C問題の自身の解答と解答説明をしていきます。
- 競技プログラミング初心者で、問題の解き方がわからない方
- AtCoderの公式解説は読んだが、内容が理解できなかった方
- Pythonでの解法を知りたい方
まだまだ学習の身ですので、最適コードではない部分も多々あるかと思いますが、その部分は同じ学習者として温かい気持ちで応援&ご助言頂けば嬉しいです。
では早速行ってみましょう!
今回の参加コンテスト(ABC353)
A問題:Buildings
問題文
N個のビルが横一列に並んでいて、左から i 番目のビルの高さは Hi です。
左から 1 番目のビルより高いビルが存在するか判定し、存在する場合その内最も左のビルは左から何番目か求めてください。
解答
n = int(input()) # ビルの数を入力
H = list(map(int, input().split())) # ビルの高さをリストとして入力
# 2番目のビルから順にチェック
for i in range(1, n):
# 1番目のビルより高いビルが見つかったらその位置を出力して終了
if H[0] < H[i]:
exit(print(i + 1))
# 高いビルが存在しない場合は -1 を出力
print(-1)考え方)
for文を用いて一番目のビルよりも高いかを判定していきます。注意点:
- for文のループをリストの1番目からにすることにより0番目をスキップ
- 回答時は、+1することにより問題の順番との整合性をとる
コード詳細
- ビルの数を入力として受け取ります。
- ビルの高さをリストとして入力します。
- 2番目のビルから順にチェックします。
- 1番目のビルより高いビルが見つかった場合、そのビルの位置を出力し、プログラムを終了します。
- もし1番目のビルより高いビルが存在しない場合、-1 を出力します。
B問題:AtCoder Amusement Park
問題(要約)
- K 人乗りのアトラクションに N グループが並んでいる。
- 各グループの人数は A_i で、すべての A_i は K 以下。
- アトラクションは次の手順で運行される:
- 空席が K 個。
- 空席が待機列先頭のグループ人数より少ない場合、アトラクションをスタート。
- そうでない場合、先頭グループをアトラクションに誘導。
- 1に戻る。
- 誘導終了までにアトラクションを何回スタートさせるか求める。
解答
n, k = map(int, input().split()) # グループ数とアトラクションの定員を入力
A = list(map(int, input().split())) # 各グループの人数をリストとして入力
cnt = 0 # アトラクションのスタート回数
passenger = 0 # 現在のアトラクションに乗っている人数
# 各グループの人数を順に処理
for a in A:
if passenger + a > k: # アトラクションに乗れる人数を超える場合
cnt += 1 # アトラクションをスタート
passenger = a # 新しいグループを次のアトラクションに乗せる
else:
passenger += a # グループをアトラクションに乗せる
# 最後に残った乗客がいる場合はアトラクションをもう一度スタート
print(cnt + 1 if passenger != 0 else cnt)考え方)
変数passengerを準備し、passenger + 今回の登場人数 が k を超えるかどうかを判断することにより、回数を数えていきます。
for文終了後においてもpassengerに乗客が残っている場合は、もう一回アトラクションを回す必要があることに注意。
コード詳細
- グループ数 n とアトラクションの定員 k を入力します。
- 各グループの人数をリスト A として入力します。
- アトラクションのスタート回数 cnt を 0 で初期化します。
- 現在のアトラクションに乗っている人数 passenger を 0 で初期化します。
- 各グループの人数 a を順に処理します。
- 現在の乗客数と次のグループの人数を合計して、定員を超える場合:
- アトラクションをスタートさせて回数を増やします。
- 次のグループを新しいアトラクションに乗せます。
- 定員を超えない場合は、グループを現在のアトラクションに乗せます。
- 最後に乗客が残っている場合は、もう一度アトラクションをスタートさせます。
C問題:Sigma Problem
問題
正整数 x,y に対して f(x,y) を「(x+y) を 108 で割ったあまり」として定義します。
長さ N の正整数列 A=(A1,…,AN) が与えられます。次の式の値を求めてください。
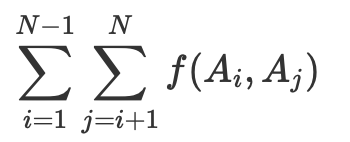
解答
import bisect
n = int(input()) # 整数列の長さを入力
A = sorted(list(map(int, input().split()))) # 整数列をソートして入力
mod = 10**8 # モジュラス
cnt = 0 # モジュラスを超えるペアのカウント
total = 0 # f(A_i, A_j) の合計
# 各要素に対して処理を行う
for i in range(n):
total += A[i] * (n-1) # 全体の合計に A[i] を (n-1) 回追加
pos = bisect.bisect_left(A, mod - A[i], i + 1) # A[i] とペアを組んで mod を超える最小の位置を見つける
cnt += n - pos # mod を超えるペアの数をカウント
print(total - mod * cnt) # 全体の合計から mod を超える部分を引くポイント)
問題文の与えられた式通りに2重のfor文で実装してしまうと、制約条件が大きいため実行制限時間超過になってしまいます。そこで下記を行なっています。
- 配列Aをソートする
- x + y ≧ 108、つまり、各xに対して y ≧ 108 – x が成り立つ個数をカウントする
- 上記のカウントにおいて二分探索を用いることにより、少ない計算で配列の位置を求める
- 求めた位置から右側は全て y ≧ 108 – x を満たす
- 108で割らない場合の合計値を算出する。各値に対して (n-1)をかけることにより求めれる
- 上記の合計値 – 108 * カウント をすることにより求めれる(Ai ≦ 108 条件のため)
解き方(詳細):
- 長さ ( n ) の整数列の長さを入力します。
- 整数列 ( A ) をソートして入力します。
- モジュラス ( 108 ) を定義します。
- モジュラスを超えるペアのカウント ( cnt ) を 0 で初期化します。
- ( f(A_i, A_j) ) の合計 ( total ) を 0 で初期化します。
- 各要素 ( A[i] ) に対して以下の処理を行います:
- ( A[i] ) を全体の合計に (n-1) 回追加します。
- ( A[i] ) とペアを組んで ( 108 ) を超える最小の位置を二分探索で見つけます。
- モジュラスを超えるペアの数をカウントします。
- 最後に、全体の合計からモジュラスを超える部分を引いた結果を出力します。
感想
今回はB問題までしか解くことができませんでした。
A問題は、1番目のビルよりも高いビルを探す問題でした。forループの範囲を1番目(0番目を含めない)から始めることで解決できました。
B問題では、アトラクションの数を数える問題でした。現在の乗客の数と次に乗ってくる乗客の数を条件に当てはめることで解決できました。問題文が長かったですが、すぐに理解して実装できました。
C問題は、与えられた二重のΣ(シグマ)の式を計算する問題でした。制約条件が大きく、通常の実装では不正解になってしまいました。効率化を図りましたが、制限時間内には答えを思いつかずに時間切れとなってしまいました。しかし、回答の考え方を参考にしつつ、自分の当初の考えも取り入れて、二分探索を用いることでようやく解決できました。
今回B問題までしか解けませんでしたが、A, B問題を素早く解けたことでレーティングが上がり547になりました。これまでの努力の成果だと思います。今後も続けていきたいと思います。
皆さんも競技プログラミングを楽しんでくださいね!(*^▽^)/


コメント